Via Jerry Coyne, I came across this exchange between Sam Harris and David Eagleman. Boring, standardized inaccuracies about the relationship between atheism, New Atheism, and certainty aside, I think that the problems with Eagleman's `Possibilianism' are deeper than Harris recognizes, insofar as such a thing is possible to say after flat-out inconsistency has been established.
The error which pervades his website and his talk is a simple one: a black/white split between commitment and non-commitment. He appears to be irretrievably mired in the old "believe X/believe not X/suspend judgment" trichotomy. Like many other three-horned creatures, this sort of thinking feels awfully... extinct. On first and other inspections, Possibilianism appears to be Bayesianism without the rigor. One simply enumerates possibilities - apparently as only emphasized for theism, though I do not see why other propositions should not be similarly attended to - and does not worry about things like analytical usefulness or Dutch-books or probabilistic consistency or positing any principled means of updating commitments. It looks like dodging and attention-getting; it smells like dodging and attention-getting; and yet here I am, about to give it a taste-test as well. I suspect this is about to get deeply unhealthy.
Perhaps Eagleman is wholly unfamiliar with analytic philosophy or the philosophy of science, despite his heavy allusions to the same. In Bayesianism, one holds `multiple ideas' in ones head, but not simply as possibilities but as articles with differing probabilities. As one of the simplest theories in probability runs, prob(X)+prob(~X)=1, a statement that generalizes to any finite partitioning of possibilities on the assumption of finite additivity, which is itself an implication of the stronger assumption of countable additivity, which itself yields an analogous result. Another popular standard, widely-assumed, is regularity, which states that all possible propositions have probability greater than 0.
So a Bayesian who accepts regularity as regards coherently formulated definitions of God is already holding the possibilities in mind. Further, the confidences allotted to the differing possibilities are reflected in one's prior whenever updating on new discoveries. One may even update on uncertain propositions using Jeffrey Conditioning. All around the world today, Bayesians are wagering on uncertainty and on propositions for which no decisive evidence exists. For all of these methods, there are various arguments, and the limits and applications of these methods are items of active research and discussion. In the absence of any evidence, equivocation is the most popular method. So, what exactly does David Eagleman have to offer?
T-shirts and confusion and "boy is this Universe is a counter-intuitive and amazing place!"
He uses terms like `likelihood' and other probabilistic language, but does not seem to understand probabilism. In this matter, he appears to be similar to (most of) the New Atheists, minus his uncomprehending overview. The New Atheists are if anything more consistent with probabilism in their language than is Eagleman.
It really is that bad. This sort of `oh look at my radical new way of thinking about knowledge (especially theistic belief)' annoys me to no end, especially when it comes in the form of a condescending lecture to us over-certain militant atheists/theists. If only we opened our minds to uncertainty and possibility! Then we'd all get along.
Whether it's the `God transcends existence' crowd or the `we need a new agnosticism crowd', the boring, ignorant element remains. Because these are all useless, they are all doomed to be fads, the passing symptoms of those who are uncomfortable with using accurate words for self-description, these being loathed due to exposure to various sorts of reaction and cheap sloganeering. "Oh I don't want to be dogmatic like those atheists," or "oh I don't want to be a fundamentalist like those theists." Those. Those. Not me. No way. They lazily search for Third Ways that already exist and in a form superior to their imaginations, or they simply wax incoherent; they pay little attention to existing criticisms, which they cannot know to be relevant because they are ignorant.
Gimme my TED talk, please! I'd love to profit from an exciting, revolutionary proposal of stuff that's been around for centuries. Hell, I'll make up my own new word for probabilism and decision theory and have my own movement. I'll call it `nicepersonopenmindednessism' or `uncertaintyisgoodpolicyism'. Goodness, I could write a book! To ensure originality, I'll fudge a few details. I'd hate to be thought a plagiarist. `Mysterianism' is already taken, alas. (I note that Mysterianism is actually worth looking at.)
Edit (9/5/2011): I would recommend reading this before watching the TED talk.
Showing posts with label probability. Show all posts
Showing posts with label probability. Show all posts
Saturday, September 3, 2011
Sunday, August 7, 2011
Trying to formalize the OTF
Via Victor Reppert, I came across another atheistic critique of the OTF by Thrasymachus. Inspired by its superior clarity, I have decided to further clarify my previous objections. Thrasymachus is also replying to a previous reply by Loftus which is better suited to my purposes than his other writings.
Thrasymachus focuses on the OTF as premised by Loftus in this post:
1. Rational people in distinct geographical locations around the globe overwhelmingly adopt and defend a wide diversity of religious faiths due to their upbringing and cultural heritage. This is the religious diversity thesis.
2. Consequently, it seems very likely that adopting one’s religious faith is not merely a matter of independent rational judgment but is causally dependent on cultural conditions to an overwhelming degree. This is the religious dependency thesis.
3. Hence the odds are highly likely that any given adopted religious faith is false.
4. So the best way to test one’s adopted religious faith is from the perspective of an outsider with the same level of skepticism used to evaluate other religious faiths. This ex-presses the OTF.
Loftus uses the phrase "the odds are highly likely" in response to the observation that a deductive equivalent of the above is invalid. But as Thrasymachus points out, it still is not clear that (3) follows from (1)/(2).
First, let me clear some fumes: I am assuming that everyone involved agrees that certainty in religious beliefs is unwarranted. I am also assuming that after this is recognized, the religious beliefs in question can be probabilized. This is not always obvious: some claims are not obviously susceptible to forceful probabilities. The doctrine of the Trinity, for example, has other conceptual issues to clear up before this may be done. Instead of throwing up our hands, we can focus on the subset of putative truths essential to Christianity (C) which can be probabilized, e.g. the Resurrection. It is the probability of these claims in conjunction that is represented by prob(C).
Second, (1) assumes that differing religious people are or can be rational, at least in the sense that their beliefs are internally consistent. Else, we have no need of the OTF, as incoherency arguments would more than suffice.
Now we can see what would be required for (3) to follow from (1) and (2). I will set as a threshold that (3)/(4) translate as requiring, at a minimum, that Christianity is not more likely to be true than not, i.e. 0.5>p(C). Denote the religious diversity thesis by Div, the religious dependency thesis by Dep, and p the prior probability of some unspecified Christian.1 The odds form of Bayes' Theorem is as follows:
.
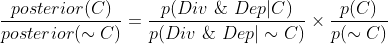To get (3)/(4) as I interpret them, we need
.
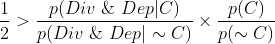In order for this to be the case, we need to know three different quantities. p(C)=1-p(~C), p(Div & Dep|C), and p(Div & Dep|~C). All we can say about p(C) is that it is greater than 1/2, as we are talking about a believer's prior. So we need something at least as strong as p(Div & Dep|~C)>p(Div & Dep|C). But as I pointed out in a previous post, not even this inequality must hold.
And so we come to the reason why I did not attempt to formalize the OTF much earlier: it simply isn't a probabilistic inference; it is a demand about priors. I think this is why Loftus has yet to put an argument about probabilities in terms of formal probabilities, as far as I can find. This is not a case of updating a prior set of rational beliefs to a new probability by reasoned argument. Instead, it is an attempt to force a reworking of priors based on evidence.2 Again, I do not see why Christians need to accept this; intellectual consistency only requires that they account for Div and Dep by calculating their effects on their beliefs through conditioning.
Here we depart from the most accepted form of Bayesianism, i.e. subjective Bayesianism, entirely. We are encountering a curious version of objective Bayesianism. `Normal' objective Bayesians calculate `informationless' priors by equivocating across possibilities. What Loftus appears to want, as I noted in my previous posts, is that we gauge p(C) in something like the following way:
a. p(C)=1/N where N is the number of possible, mutually contradictory religions.
b. p(C)=1/N where N is the number of mutually contradictory religions in human history.
c. p(C)=1/N where N is the number of existing, mutually contradictory religions.
[Each of the above has an analogue where `religions' is replaced by `Christian sects'.]
d. p(C)=x where x is the frequency of the occurrence of Christians with respect to the general population. (Of the country, or world, or something.)
e. p(C)=A/B where B is the number of rational people and A is the number of rational people who are Christians.
And so on. Before moving on, the first response our Christian might deploy to any combination of the above is a simple one: No.
He is presumed to be rational and he can account for (1)/(2) in the usual way. Sorry to wax tautological, but he simply cannot be convicted of irrationality or unreasonableness whenever he is being both rational and reasonable, as judged by standard philosophical criteria. To go further with this, Loftus will have to mount a convincing attack on Bayesianism itself.
And of course we run into the earlier problem yet again; the argument Loftus presents cannot be probabilized. None of the above statements follows, or can follow, deductively or probabilistically, from (1)/(2).
I could continue on about the other problems, especially as they pertain to Loftus' desire to demand priors about religion but not about secular claims, or that this approach would most likely result in a weaker case against Christianity than the traditional arguments, but I've said this already, and Thrasymachus has done a better job explicating it. I could repeat why `skepticism' is not a sort of default, and that positive claims will be necessary to argue against Christianity. (Otherwise, it's the fallacy of probabilistic Modus Tollens all the way down.) Or, I could reiterate some of Reppert's objections; for example, (1) and (2) are not so undeniably true as Loftus suggests, and Christians may account for differing religions using faith-based claims. The Pharaoh's magicians did not perform wonders so great as Aaron's, but they still made a snake out of a staff. Also, demons and sinful nature.
I pause. Is the argument really this straightforwardly awful? How does Loftus defend it?
What else can I say? Nothing about this argument works, nor could it conceivably be reworked to capture what Loftus wants. There's a reason for this: it isn't actually an argument. It is a symptom of Loftus' assumption that he objectively and most accurately views the world in a culture-transcendent way.
I might have spoken too soon: if a Christian happens to trust Loftus more than God, there may be an opening for the OTF.
One last quibble to anticipate an objection: Loftus may claim that he is not addressing Calvinists, only evangelical Christians. That doesn't change the fact that his argument is not even an argument of that form. For this discrepancy to matter, he must restate his argument so as to account for variations in prior probability and variations in the Bayes factor specific to the religion in which he is interested. That is, he must pursue normal argumentation.
If he does so, I'll be more than happy.
1. It has to be this way, as we are interested in whether or not warrant for religion can be retained, not just how a skeptic feels about religion.
2. This is much weirder than anything attempted by normal objective Bayesians. I do not know of any accepted precedent for an approach like this.
Edit 8/8/11: I've been having a blast with acronyms lately. Please plagiarize the hell out of this excerpt from a comment at Reppert's place:
Thrasymachus focuses on the OTF as premised by Loftus in this post:
1. Rational people in distinct geographical locations around the globe overwhelmingly adopt and defend a wide diversity of religious faiths due to their upbringing and cultural heritage. This is the religious diversity thesis.
2. Consequently, it seems very likely that adopting one’s religious faith is not merely a matter of independent rational judgment but is causally dependent on cultural conditions to an overwhelming degree. This is the religious dependency thesis.
3. Hence the odds are highly likely that any given adopted religious faith is false.
4. So the best way to test one’s adopted religious faith is from the perspective of an outsider with the same level of skepticism used to evaluate other religious faiths. This ex-presses the OTF.
Loftus uses the phrase "the odds are highly likely" in response to the observation that a deductive equivalent of the above is invalid. But as Thrasymachus points out, it still is not clear that (3) follows from (1)/(2).
First, let me clear some fumes: I am assuming that everyone involved agrees that certainty in religious beliefs is unwarranted. I am also assuming that after this is recognized, the religious beliefs in question can be probabilized. This is not always obvious: some claims are not obviously susceptible to forceful probabilities. The doctrine of the Trinity, for example, has other conceptual issues to clear up before this may be done. Instead of throwing up our hands, we can focus on the subset of putative truths essential to Christianity (C) which can be probabilized, e.g. the Resurrection. It is the probability of these claims in conjunction that is represented by prob(C).
Second, (1) assumes that differing religious people are or can be rational, at least in the sense that their beliefs are internally consistent. Else, we have no need of the OTF, as incoherency arguments would more than suffice.
Now we can see what would be required for (3) to follow from (1) and (2). I will set as a threshold that (3)/(4) translate as requiring, at a minimum, that Christianity is not more likely to be true than not, i.e. 0.5>p(C). Denote the religious diversity thesis by Div, the religious dependency thesis by Dep, and p the prior probability of some unspecified Christian.1 The odds form of Bayes' Theorem is as follows:
To get (3)/(4) as I interpret them, we need
In order for this to be the case, we need to know three different quantities. p(C)=1-p(~C), p(Div & Dep|C), and p(Div & Dep|~C). All we can say about p(C) is that it is greater than 1/2, as we are talking about a believer's prior. So we need something at least as strong as p(Div & Dep|~C)>p(Div & Dep|C). But as I pointed out in a previous post, not even this inequality must hold.
At the end of my last post, I asked a question: what would Calvin think of the OTF? It wasn't an idle question. If you are a Christian who believes in the predestination of the Elect and the Fallen world, the fact that your religion is one amongst many is not a surprise. That few have the right faith may not bother you at all. As far as I am aware, nothing about your religion says that it should not appear to an outsider as one among many. Strange then that advocates of the OTF tell you that the existence of other religions discredits your religion. You can reasonably say, "my religion looks like one of many to you? Swell, your point being? We agree about this, and it bothers me not. For chances are that you are not one of the Elect and are not destined for Salvation and understanding. That you and others do not believe as I do does not surprise me in the least; if anything, I would be surprised if outsiders readily understood the Truth and could easily aspire to it, as I understand otherwise."But it gets worse: even in the cases where the requisite inequality does hold, it may not be large enough to require our believer to make further arguments so as to defend his faith. This is because we still need to know what values of p(C) are warranted. Sure, it's less than 1, but is it less than 0.999 or 0.8?
One can argue against such a person, but the appearance of his beliefs to a skeptic should not itself constitute an argument.
The case is different whenever we look at more common evangelical versions of Christianity, in which it is asserted that God intervenes or has intervened to aid Christianity and that the Holy Spirit works on the consciences of most or all to guide them to Truth. Free will. All that jazz. If a supernatural agency is at work in the Christian sociology of Christianity, then it is surprisingly hidden in the actual sociological details concerning Christianity. Here, the fact that Christian belief is largely a function of geography and parenting is very surprising. To a person who thinks that Christianity is a natural phenomenon, it should not be. I think that this is a very powerful argument against evangelical Christianity.
Notice then that there are at least two possible outcomes of "Christianity is like other religions to an outsider": it is irrelevant to some Christians, and it constitutes a challenging argument to others. So what we can not do is treat the motivations for the OTF as legitimizing it against religions generally, since the observations motivating the OTF are in no way an argument against certain religions. To pretend otherwise is to do nothing more than pomo an important, but narrow, point.
And so we come to the reason why I did not attempt to formalize the OTF much earlier: it simply isn't a probabilistic inference; it is a demand about priors. I think this is why Loftus has yet to put an argument about probabilities in terms of formal probabilities, as far as I can find. This is not a case of updating a prior set of rational beliefs to a new probability by reasoned argument. Instead, it is an attempt to force a reworking of priors based on evidence.2 Again, I do not see why Christians need to accept this; intellectual consistency only requires that they account for Div and Dep by calculating their effects on their beliefs through conditioning.
Here we depart from the most accepted form of Bayesianism, i.e. subjective Bayesianism, entirely. We are encountering a curious version of objective Bayesianism. `Normal' objective Bayesians calculate `informationless' priors by equivocating across possibilities. What Loftus appears to want, as I noted in my previous posts, is that we gauge p(C) in something like the following way:
a. p(C)=1/N where N is the number of possible, mutually contradictory religions.
b. p(C)=1/N where N is the number of mutually contradictory religions in human history.
c. p(C)=1/N where N is the number of existing, mutually contradictory religions.
[Each of the above has an analogue where `religions' is replaced by `Christian sects'.]
d. p(C)=x where x is the frequency of the occurrence of Christians with respect to the general population. (Of the country, or world, or something.)
e. p(C)=A/B where B is the number of rational people and A is the number of rational people who are Christians.
And so on. Before moving on, the first response our Christian might deploy to any combination of the above is a simple one: No.
He is presumed to be rational and he can account for (1)/(2) in the usual way. Sorry to wax tautological, but he simply cannot be convicted of irrationality or unreasonableness whenever he is being both rational and reasonable, as judged by standard philosophical criteria. To go further with this, Loftus will have to mount a convincing attack on Bayesianism itself.
And of course we run into the earlier problem yet again; the argument Loftus presents cannot be probabilized. None of the above statements follows, or can follow, deductively or probabilistically, from (1)/(2).
I could continue on about the other problems, especially as they pertain to Loftus' desire to demand priors about religion but not about secular claims, or that this approach would most likely result in a weaker case against Christianity than the traditional arguments, but I've said this already, and Thrasymachus has done a better job explicating it. I could repeat why `skepticism' is not a sort of default, and that positive claims will be necessary to argue against Christianity. (Otherwise, it's the fallacy of probabilistic Modus Tollens all the way down.) Or, I could reiterate some of Reppert's objections; for example, (1) and (2) are not so undeniably true as Loftus suggests, and Christians may account for differing religions using faith-based claims. The Pharaoh's magicians did not perform wonders so great as Aaron's, but they still made a snake out of a staff. Also, demons and sinful nature.
I pause. Is the argument really this straightforwardly awful? How does Loftus defend it?
One...option for the Christian might be to argue that I have not shown there is a direct causal relationship between RDPT (i.e. the Religious Dependency Thesis) (or 1) and the RDVT (i.e., the Religious Diversity Thesis) (or 2). Just because there is religious diversity doesn’t mean that religious views are overwhelmingly dependent on social and geographical factors, they might argue. Reminiscent of David Hume, who argued that we do not see cause and effect, they might try to argue I have not shown it exists between the RDPT and the RDVT. After all, if Hume can say he never sees one billiard ball “causing” another one to move just because they do so after making contact, then maybe there is no direct causal relationship between the RDPT and the RDVT. Is it possible, they might ask, that just because people have different religious faiths which are separated into distinct geographical locations on our planet, that “when and where” people are born has little to do with what they believe? My answer is that if this is possible, it is an exceedingly small possibility. Do Christians really want to hang their faith on such a slender reed as this? I’ve shown from sociological, geographical and psychological studies that what we believe is strongly influenced by “the accidents of history.” That’s all anyone can ask me to show.Actually, we can ask for a valid argument. This is simply a genetic fallacy. The deductive genetic fallacy remains a fallacy, even if you argue for odds instead of certainties.
What else can I say? Nothing about this argument works, nor could it conceivably be reworked to capture what Loftus wants. There's a reason for this: it isn't actually an argument. It is a symptom of Loftus' assumption that he objectively and most accurately views the world in a culture-transcendent way.
I might have spoken too soon: if a Christian happens to trust Loftus more than God, there may be an opening for the OTF.
One last quibble to anticipate an objection: Loftus may claim that he is not addressing Calvinists, only evangelical Christians. That doesn't change the fact that his argument is not even an argument of that form. For this discrepancy to matter, he must restate his argument so as to account for variations in prior probability and variations in the Bayes factor specific to the religion in which he is interested. That is, he must pursue normal argumentation.
If he does so, I'll be more than happy.
1. It has to be this way, as we are interested in whether or not warrant for religion can be retained, not just how a skeptic feels about religion.
2. This is much weirder than anything attempted by normal objective Bayesians. I do not know of any accepted precedent for an approach like this.
Edit 8/8/11: I've been having a blast with acronyms lately. Please plagiarize the hell out of this excerpt from a comment at Reppert's place:
I should mention that I've seen John's post that he's on a blogging break, so I do not expect any response soon.
To be honest, I don't expect a serious response. Here's what he said to Thrasymachus' post back in January:
"I see nothing here I need to respond to."
Oh, my argument is invalid, cannot be reworked to convincingly get what I want out of it, and my approach in general is a failure. Where's the problem?
Staggering. And this is followed by another unhesitant shift:
"You can insert the word “skeptical” for “outsider” if you wish. And being skeptical means doubting or rejecting anything that the sciences say otherwise."
And we return to the uniqueness problems and question-begging again...
So I'll have fun at his expense until he or others get back to me with a real argument. A satisfactory response will do the following things:
1. Restatement: the precise structure and intended conclusion(s) of the OTF must be clearly stated, along with any contested background assumptions.
2. Support: The structure and conclusions of the argument must be corroborated. Is it deductive? If so, state exactly where and why. Is it a probabilistic argument? Then capture the argument using the formal tools of probabilism and defend it. Is it an argument about prior distributions? Then state clearly why it is that a coherent agent must adopt, prior to evidence, a specific distribution based on an observation which can already accounted for by a religious person or may be calibrated in a traditional, probabilistic manner (conditionalization).
3. Comprehensiveness: Clearly state outstanding objections and why they fail or are otherwise innocuous.
I call it the Simple Test For Understanding, or STFU, because proponents of the OTF should STFU already or move on.
Friday, August 5, 2011
An unconfirmability argument
[A caution: This post is long, verbose, and overly technical. Read the dialogue I posted at the end. If it is comprehensible to you, you should have an adequate grasp of the contents of this and the previous post.]
In my last post, I interpreted Hume's argument against the confirmability of miracles and found it to be unsound. Now I want to affirmatively answer another question: given that Hume's argument is unconvincing, is there another unconfirmability argument which applies to paradigm miracles like the Resurrection?
If so, we are not doomed to Earman's (apparent) conclusion, that we must analyze the details of every miracle claim if we are to safely reject miracles (p.3). Rather, we can specify categories of claims, narrower than `miracle', that cannot be confirmed by certain categories of evidence. Though we might not safely assert something like "no evidence you have should convince me of a miracle," we may be able to say something like "by itself, the evidence you present is by nature incapable of overcoming the prior probability of the type of miracle you assert." I will leave open the possibility that miracles like the Resurrection (R) can be confirmed; I am only closing a class of potential means of doing so. I do not think that I am providing or can provide "an everlasting check to all kinds of superstitious delusion" which "will be useful as long as the world endures" (EPHU, p.169); rather, I am giving something which, if successful, would obviate any non-pedagogical, rational need for any detailed Bayesian analysis of the Resurrection like this one, so long as we lack other significant arguments in favor of Christianity. One notices the number of qualifiers required to invest in such an argument, and there will be more. This form of argument does not constitute a license for ignorance, and it will require creative adaption to specific miracle claims.
A lot hinges on the problem of determining appropriate priors in subjective Bayesianism. In order to provide some convincing estimate of the prior odds on R, a trick - I think novel to me - must be applied.
To motivate this trick, I'll cite its precedent and inspiration: the method of reparation, originally due to Richard Jeffrey. This tool was invented for a specific problem, the problem of old evidence. Roughly, the problem is as follows: whenever a new theory is crafted, its ability to explain known phenomenon is considered to be of epistemic significance. For example, relativity theory's ability to `predict' the perihelion precession of Mercury - a phenomenon which had long defied explanation in classical physics - is considered powerful evidence for that theory. But the hypothetico-deductive principle, which states that verification of an uncertain prediction of an uncertain hypothesis increases the probability of that hypothesis, is incapable of yielding this well-founded intuition; the `prediction' is already known, i.e. not uncertain.
Reparation solves this problem by positing a hypothetical prior probability, an ur-distribution or ur-prior, in which the theoretical prediction itself in addition to the corresponding observation is treated as uncertain. The `discovery' of that implication and the evidence then raises the probability of the hypothesis in question in a straightforward way. I want to extend this to a problem which plagues estimating the prior probability of miracles, i.e. the problem of old evidence and explanation, or if you prefer, the old everything problem. When priors are not in dispute, this method is unnecessary; this is not an actual case of confirmation. But on the very safe assumption that the prior probability of R, in the absence of other argument, is calibrated with respect to confirmation of natural principles, it is quite useful. We `know' that the prior ratio is small, but we do not know how small. This is important when disputes depend on whether or not that prior is greater than 1/1000 or less than 10-44. We need something better than the `vague intuitions' rightly deplored by the McGrews (CCRJ, p.50).
The idea is to posit an ur-prior u which is (partially) devoid of current background knowledge. The voided background knowledge is treated as uncertain in u, the recapturing of which yields through conditionalization a suitable prior p. In this context, the `recaptured' knowledge is the bulk of the `uniform evidence of sense' discussed by Hume, which is assumed to be wholly confirmatory of the law L. As I am working with the Resurrection, L is the principle that dead people remain dead. By definition and subset rule, we have for any probability pr that
\leq pr(\sim R),pr(R)\leq pr(\sim L)\} "\{L\longrightarrow\sim R,\ R\longrightarrow\sim L\}\implies \{pr(L)\leq pr(\sim R),pr(R)\leq pr(\sim L)\}")
.
By quick algebra, we yield the following inequality:
}{pr(\sim R)}\leq \frac{pr(\sim L)}{pr(L)} "\frac{pr(R)}{pr(\sim R)}\leq \frac{pr(\sim L)}{pr(L)}")
.
So by calculating our confidence in L, we set a maximum confidence in R.
As I mentioned, we want to `recapture' p using u by conditioning, that is,
}{p(\sim R)}\leq \frac{p(\sim L)}{p(L)}=\frac{u(O|\sim L)}{u(O|L)}\times \frac{u(\sim L)}{u(L)}=u(O|\sim L)\times \frac{u(\sim L)}{u(L)} "\frac{p(R)}{p(\sim R)}\leq \frac{p(\sim L)}{p(L)}=\frac{u(O|\sim L)}{u(O|L)}\times \frac{u(\sim L)}{u(L)}=u(O|\sim L)\times \frac{u(\sim L)}{u(L)}")
,
where O is the set of observations confirming the putative law. But here I seem to have merely shifted the problem elsewhere, since we now need the u-odds on ~L. This regress is halted by the following abstract consideration: at some theoretical point of time, a hypothetical rational agent should have crossed the `more likely than not' threshold in favor of the law. For this reason, we may assume that the u-odds on ~L is 1. From there we must estimate the raw confirmatory force of the remaining experience as captured by the u-Bayes factor. Cleaning up the previous mess, we want to analyze
}{p(\sim R)}\leq u(O|\sim L) "\frac{p(R)}{p(\sim R)}\leq u(O|\sim L)")
.
Now here is the crucial question: what does ~L look like after this partial recapitulation of background knowledge? An `anti-law' which states that all dead people resurrect will have probability zero, but this is an extreme; the preexisting information will select for those non-laws which ascribe higher probability to individual non-resurrections. These include, amongst other things, statements like "everybody who dies remains dead except under very rare conditions." However, even this will be made less probable by O so long as the further prediction of its elements are uncertain. Unless one claims to be able to specify in advance who should be exempted from death based on limited confirmation, the effect remains strong as regards statements like "everybody stays dead except for Jesus." (Lazarus and other proposed resurrections are not part of the background knowledge being recaptured here.)
To go further, I assume that O contains N instances of confirmation beyond those which lead our hypothetical agent to equivocate, each of which are of equal weight1, i.e.
=u(O_j|\sim L)\forall i,j\in[N] "O=\{O_1,...,O_N\}\text{ and }u(O_i|\sim L)=u(O_j|\sim L)\forall i,j\in[N]")
where I use the combinatorial notation [N]={1,...,N} for the sake of cleanliness. Supposing that each element of O is independent modulo ~O, we have that
=u(O_1|\sim L)^N "u(O|\sim L)=u(O_1|\sim L)^N")
.
So if N=106, even a quite large value for u(O1|~L) yields an absurdly small upper bound on the prior odds on R. If this assumption of independence is to fail in favor of the theists, there must be in the domain of u some significant set of propositions in ~L that correlate the elements of O. In other words, there must be plausible causal processes not implying L which probabilistically tend to keep dead people dead.
And here is where the remainder of our scientific knowledge and experience come into play. We do not consider L to be a fundamental feature of the universe but a consequence of other properties. Were a technology developed that allowed for the reanimation of corpses, we need not say that a putative law of nature had been overturned; instead, we would say that the `ordinary course' had been altered by the introduction of a new yet naturalistic element. Without such technology, we expect other principles to produce L. These include thermodynamic principles. When Jesus died, there are three sorts of miraculous possibilities: either his vital tissues never fatally decayed by supernatural sustenance, his vital tissues decayed but were reconstituted gradually or suddenly prior to his reanimation, or he reanimated without the function of his vital organs. Each of these possibilities runs against other established regularities. Properly speaking, then, L is not merely the generalized rule that dead people remain dead but also the set of combinations of rules which produce that outcome. For the Resurrection to occur, every one of those combinations must fail to hold.
So a theory which advantageously counters the above independence assumption must probabilistically correlate the elements of O, have significant plausibility in its own right, and fail to assume or imply any element in L, be it the putative law itself or any combination of principles which produce that law. In this case and in the case of other miracles which violate mass/energy conservation and/or thermodynamic principles, we must toss out modern science before examining any evidence proposed against its principles. This is an absurd task, but that absurdity is consequent to proposing a suspension of the natural order.
In such a manner I tentatively maintain that the independent assumption as employed is valid in establishing an estimated upper bound on the prior odds on R. So long as we agree that it is disgustingly low, a precise value is unimportant for the strengthening of the argument. Since as you may have noticed this method of unconfirmability argument requires some detailed information concerning the relevant miracle, specifying any particular value is unimportant. For an approximate value's import to materialize, we must also delve into the category of evidence in play.
Hume appears to recognize the need for categorical bounds on the strength of evidence in his essay:
Now I must specify what I mean by a categorical bound in formal terms: roughly, a categorical bound B is a real number such whenever evidence E for an uncertain hypothesis H lies in a set C, any Bayes factor produced by E is less than or equal to B.2 That is,
}{p(E|\sim H)}\leq B "E\in C\implies \frac{p(E|H)}{p(E|\sim H)}\leq B")
.
If H is a miracle claim violating a putative law L supported by recaptured observations O, then tautologically the argument is successful if
}{p(L)}\right]^{-1}=\frac{p(L)}{p(\sim L)}=\frac{u(L|O)}{u(\sim L|O)}. "B\leq\left[\frac{p(\sim L)}{p(L)}\right]^{-1}=\frac{p(L)}{p(\sim L)}=\frac{u(L|O)}{u(\sim L|O)}.")
.
What remains is to show that the evidence proposed by the miracle-claimant lies in such a set C.
What would C look like? If we want to be trivial, we can use uncontroversial examples. For example, two gamblers who have vastly differing prior odds on the fairness of a coin should not be able to resolve their dispute by tossing the coin a small number of times to check the outcomes. With precise values available, one could derive the minimum number of tosses which could possibly result in agreement.
One may extend this notion by thinking of the epistemic limitations on experiments like "tossing a coin a certain number times" as instances of methodological bounds. In the medical sciences, anecdotal and testimonial evidence as applied to broad categories of claims is almost completely useless for confirmation; careful study is required. What this reflects is a well-founded confidence in systematic errors frequently present in anecdotal reports which cannot be sufficiently discounted in the absence of controlled study. Anecdotal evidence for a novel, popular medical hypothesis cannot by nature discount those established theories and credences, a task which is necessary in order to confirm the new remedy against a significant prior implausibility.
Similar considerations apply to many classes of potential miracles and the evidence most commonly presented for them. With the Resurrection, we need not attempt the task Hume appears to set for himself in arguing that any set of witness testimony is incapable of producing convincingly calibrated Bayes factors above something like 101000. In this case, we may instead suggest that the methods of historians in establishing the historicity of those reports and their background, while possibly very good, are not so good as to allow a confident assertion that the historical record produces a Bayes factor above 101000. Myth and utter fabrication, even if wildly improbable in this case, have precedents, and I do not think they are capable of being discarded with absolute or nearly absolute confidence given the difficulties in method.
Hoping my proposals have been convincing thus far, I conclude by giving the sort of conversation which two Bayesians could have.
Christian: Ah, skeptic! Just the person I was wanting to see! I have crafted a convincing case that the Resurrection did in fact occur, and I was wanting your feedback.
Skeptic: That sounds very interesting, but before we go into the details, would you consider the Resurrection, had it occurred, to have constituted a suspension of the natural order?
Christian: Certainly, as you well know. Otherwise, the Resurrection would be meaningless. If Jesus' Resurrection were, say, a mere product of absurdly unlikely but possible quantum fluctuations, then any argument to theism or Christianity from that event would be undermined. It would be an isolated physical anomaly; nothing more, nothing less, and surely not a communicative sign of divine endorsement of the validity of Jesus' teachings.
Skeptic: I'm glad that you and I agree. And within this possibly suspended natural order, would you admit that local, epistemic generalizations hold and that tremendous confidence in those generalizations is yielded by what Hume would call `uniform sense data'?
Christian: While I obviously do not accept Hume's argument, I agree that incredulity prior to the examination of the evidence is wholly reasonable. That is why I have analyzed the evidence; one cannot say prior to analysis whether or not the evidence is sufficient or insufficient. You and I both know that this is merely a matter of probability.
Skeptic: I do not accept Hume's argument either, but one may with certain conditions be able to obviate the need to examine all of the details in advance by grounding a posteriori bounds on Bayes factors produced by certain types of evidence.
Christian: Part of this worries me, as it sounds like an excuse to avoid examining the evidence, which, as a good skeptic and Bayesian, you should be interested in doing. In any case, I suspect that such an approach would undermine important areas of scientific research, were it to be accepted.
Skeptic: I admit that this idea is a time-saver and has its ideological attractions, but allow me to specify some of those conditions. Hopefully, when you are satisfied with their stringency, your worries will vanish. But before I may do so, I nevertheless must know the nature of the argument that you are proposing. As I said before, the bounds to which I refer would be a posteriori, not some analytic consequence of Kolmogorov's axioms, uncontroversial metaphysical theses, or sound subjective Bayesian principles. I could not pretend to Hume's rhetoric and claim "an everlasting check to all kinds of superstitious delusion," or claim to have silenced any potential reasoned argument on your part or the part of your comrades in arms, be they future comrades or present confederates. In order to state exactly what I can say in advance of detailed analysis, I have to consider at least some of the details.
Christian: That at least sounds more interesting than another platitudinous regurgitation of Hume's breathless meanderings. Fine, I will play along. I am arguing, as against many prominent skeptics, to and from the historicity of the texts with respect to several key facts, especially those facts concerning the secular claims of witness testimony.
Skeptic: Have you accorded these facts certainty in your analysis as opposed to a more general analysis, for example using Jeffrey conditioning or classical conditioning on a partition of the historical possibilities?
Christian: For the facts concerning the witnesses, I strengthened the relevant arguments so as to make those facts not only plausible, but so overwhelmingly likely as to ensure that errors of omission do not seriously undermine the strength of the argument.
Skeptic: How overwhelmingly likely?
Christian: I think that I see roughly where you are heading with this. By your earlier hintings, it is clear that you are relying on some estimate of the prior odds of the Resurrection. Riddle me this: How do you propose to estimate prior odds on the Resurrection in any convincing way? You and I are both critics of equivocation and objective Bayesianism. You and I both acknowledge the limitations of current theories of calibration, especially as applied to claims like the Resurrection.
Skeptic: Properly speaking, I do no such thing.
Christian: Help me out here.
Skeptic: I rely on the notion that miracles, to occur, require a suspension of the natural order. As you have probably anticipated, I rely on the epistemic status of that natural order with respect to any potential exemption to gauge a suitable prior on the Resurrection...
Christian: Sorry to interrupt, but clearly you seem to be contradicting yourself.
Skeptic: Only if you assume that I need a specific range of prior odds. Instead, I use the deductive implications of putative laws to straightforwardly derive inequalities via the subset rule which by basic algebra translate into an upper bound on the prior odds of the Resurrection. I only need inequalities and bounds, not specific, well-defined ranges of reasonable discussion.
Christian: Ah, I see. You're assuming that the only relevant calibrating factor is the relation of a potential suspension of the natural order to the epistemic status of the natural order, of course.
Skeptic: That's right; hence why I do not claim that my approach, even if valid, would constitute the end of the discussion. One may still need to engage the evidence, but only if an adequate, well-established natural theology is formulated so as to calibrate the priors differently.
Christian: Which of course would present a serious difficulty, since the primary and standard means of evidentially filtering Christianity out of the more general category of theism is by arguing for the Resurrection. Now I am curious: supposing you could bound the prior odds on the Resurrection below 10-1000, what would you say to me if I claimed to have produced a Bayes factor based on a confidence some salient facts which is greater than 101000?
Skeptic: I would say that you have proposed the a posteriori equivalent of proving the rationality of the square root of two, Euler's number, or pi.
Christian: That's quite a strong statement; how do you mean it?
Skeptic: I might agree that your proposed facts are plausible, even extremely convincing. But I would nevertheless insist that they cannot be sufficiently plausible as to yield such a factor. Formally, I would put evidence like that you have proposed into a set of similar evidences and claim that Bayes factors in favor of the Resurrection produced by an element in that set are below 101000.
Christian: In which case, your argument would be tautological or trivial unless you can convincingly establish, before engaging all of the details, that my textual evidence cannot be stronger. Again, I do not see how you are avoiding the shortcomings of Hume.
Skeptic: Well, you have surely noted my insistence on your specifying the type of evidence in question. I doubt you fail to imagine how that might be relevant.
Christian: I have a rough idea: are you proposing theses, like those of Hume, against testimonial evidence? Just because testimonial evidence is always subject to some precedented, possible counter-thesis, that does not mean that one can say that testimonial evidence as a category must be at least this or that weak by that virtue. The details decide how significant those considerations need to be.
Skeptic: I agree, which is another reason why I do not claim to be vindicating Hume's essay. `Testimonial evidence' is perhaps too broad a category to be subject to sufficiently small, convincing categorical boundaries. As I said before, some specifics are required. Allow me to motivate those which apply to the textual record on which you plan to rely: you can envision cases where an experiment, by its nature, cannot overcome discrepancies in prior odds so as to yield agreement between two rational agents, correct?
Christian: In highly idealized scenarios like fair dice rolls or well-understood machines and programs, sure, but I do not see the relevance to a scenario so complex and multivariate as eyewitness testimony.
Skeptic: You may at least be able to anticipate a generalization of simple and uncontroversial lessons to broader notions like `historical methodology', correct?
Christian: Not exactly, as I see such a category as too vague to easily bound.
Skeptic: Again, it depends on specifics. What is the method which you used to arrive at your initial, secular factual claims? Presumably, you do not claim to have directly observed the events in question.
Christian: Of course not.
Skeptic: And so there is some significant uncertainty in the indirect inference methods, i.e. historical methods, which you employ?
Christian: At least in a trivial sense, but that need not translate into any boundary.
Skeptic: Actually, it does, unless you claim that there is no minimally significant alternative to your facts which your methods can not diminish to an arbitrary degree. For example, can you rule out as strongly as you like the possibilities of fraud and later myth-making with respect to these secular facts?
Christian: I wouldn't say that, but again, I see no reason why, in advance, I can not devalue such possibilities sufficiently as to overcome the prior implausibility of the Resurrection.
Skeptic: If by `in advance' you mean in advance of all background knowledge, surely you are correct, but I mean the reliability of your methods with respect to our current knowledge about its reliability. If that reliability is such that the probabilities of hypotheses like frauds and myths cannot be convincingly grounded below 10-1000, I have established my case. For such extreme values, I would say that this can be said further in advance than I need to argue, but to firmly secure your methods into the category which I require, I will need to know a few more specifics.
Christian: I think I understand now, and I think that I see how you will be able to secure your conclusions were I to spell out more details. I suppose that I will have to qualify my paper with a placeholder for the time being and play with the formalisms to double-check your statements.
Skeptic: That sounds fine. In the meantime, I would be happy to read your paper. After all, you might be able to calibrate the relevant priors differently. It is still worth reading, for this and other reasons, if your conclusions are as strongly supported as you have suggested.
Christian: I look forward to your review. However, I hope you only resume technical blogging after all that wine you just drank leaves your system.
Skeptic: You're breaking the fourth wall.
1. The simplifying assumption of equal-weightedness is not generally true. If alternatives to the law include something like `dead people remain dead unless you perform a certain magic ritual', then only failures of that ritual will contrast the hypothesis with L. We can recapture the plausibility of the assumption by stipulating that a theoretical agent at this theoretical threshold point has effectively ruled any particular such hypothesis.
2. I've been playing with this notion for some time, and I know of several generalizations if anyone is interested.
In my last post, I interpreted Hume's argument against the confirmability of miracles and found it to be unsound. Now I want to affirmatively answer another question: given that Hume's argument is unconvincing, is there another unconfirmability argument which applies to paradigm miracles like the Resurrection?
If so, we are not doomed to Earman's (apparent) conclusion, that we must analyze the details of every miracle claim if we are to safely reject miracles (p.3). Rather, we can specify categories of claims, narrower than `miracle', that cannot be confirmed by certain categories of evidence. Though we might not safely assert something like "no evidence you have should convince me of a miracle," we may be able to say something like "by itself, the evidence you present is by nature incapable of overcoming the prior probability of the type of miracle you assert." I will leave open the possibility that miracles like the Resurrection (R) can be confirmed; I am only closing a class of potential means of doing so. I do not think that I am providing or can provide "an everlasting check to all kinds of superstitious delusion" which "will be useful as long as the world endures" (EPHU, p.169); rather, I am giving something which, if successful, would obviate any non-pedagogical, rational need for any detailed Bayesian analysis of the Resurrection like this one, so long as we lack other significant arguments in favor of Christianity. One notices the number of qualifiers required to invest in such an argument, and there will be more. This form of argument does not constitute a license for ignorance, and it will require creative adaption to specific miracle claims.
A lot hinges on the problem of determining appropriate priors in subjective Bayesianism. In order to provide some convincing estimate of the prior odds on R, a trick - I think novel to me - must be applied.
To motivate this trick, I'll cite its precedent and inspiration: the method of reparation, originally due to Richard Jeffrey. This tool was invented for a specific problem, the problem of old evidence. Roughly, the problem is as follows: whenever a new theory is crafted, its ability to explain known phenomenon is considered to be of epistemic significance. For example, relativity theory's ability to `predict' the perihelion precession of Mercury - a phenomenon which had long defied explanation in classical physics - is considered powerful evidence for that theory. But the hypothetico-deductive principle, which states that verification of an uncertain prediction of an uncertain hypothesis increases the probability of that hypothesis, is incapable of yielding this well-founded intuition; the `prediction' is already known, i.e. not uncertain.
Reparation solves this problem by positing a hypothetical prior probability, an ur-distribution or ur-prior, in which the theoretical prediction itself in addition to the corresponding observation is treated as uncertain. The `discovery' of that implication and the evidence then raises the probability of the hypothesis in question in a straightforward way. I want to extend this to a problem which plagues estimating the prior probability of miracles, i.e. the problem of old evidence and explanation, or if you prefer, the old everything problem. When priors are not in dispute, this method is unnecessary; this is not an actual case of confirmation. But on the very safe assumption that the prior probability of R, in the absence of other argument, is calibrated with respect to confirmation of natural principles, it is quite useful. We `know' that the prior ratio is small, but we do not know how small. This is important when disputes depend on whether or not that prior is greater than 1/1000 or less than 10-44. We need something better than the `vague intuitions' rightly deplored by the McGrews (CCRJ, p.50).
The idea is to posit an ur-prior u which is (partially) devoid of current background knowledge. The voided background knowledge is treated as uncertain in u, the recapturing of which yields through conditionalization a suitable prior p. In this context, the `recaptured' knowledge is the bulk of the `uniform evidence of sense' discussed by Hume, which is assumed to be wholly confirmatory of the law L. As I am working with the Resurrection, L is the principle that dead people remain dead. By definition and subset rule, we have for any probability pr that
By quick algebra, we yield the following inequality:
So by calculating our confidence in L, we set a maximum confidence in R.
As I mentioned, we want to `recapture' p using u by conditioning, that is,
where O is the set of observations confirming the putative law. But here I seem to have merely shifted the problem elsewhere, since we now need the u-odds on ~L. This regress is halted by the following abstract consideration: at some theoretical point of time, a hypothetical rational agent should have crossed the `more likely than not' threshold in favor of the law. For this reason, we may assume that the u-odds on ~L is 1. From there we must estimate the raw confirmatory force of the remaining experience as captured by the u-Bayes factor. Cleaning up the previous mess, we want to analyze
Now here is the crucial question: what does ~L look like after this partial recapitulation of background knowledge? An `anti-law' which states that all dead people resurrect will have probability zero, but this is an extreme; the preexisting information will select for those non-laws which ascribe higher probability to individual non-resurrections. These include, amongst other things, statements like "everybody who dies remains dead except under very rare conditions." However, even this will be made less probable by O so long as the further prediction of its elements are uncertain. Unless one claims to be able to specify in advance who should be exempted from death based on limited confirmation, the effect remains strong as regards statements like "everybody stays dead except for Jesus." (Lazarus and other proposed resurrections are not part of the background knowledge being recaptured here.)
To go further, I assume that O contains N instances of confirmation beyond those which lead our hypothetical agent to equivocate, each of which are of equal weight1, i.e.
where I use the combinatorial notation [N]={1,...,N} for the sake of cleanliness. Supposing that each element of O is independent modulo ~O, we have that
So if N=106, even a quite large value for u(O1|~L) yields an absurdly small upper bound on the prior odds on R. If this assumption of independence is to fail in favor of the theists, there must be in the domain of u some significant set of propositions in ~L that correlate the elements of O. In other words, there must be plausible causal processes not implying L which probabilistically tend to keep dead people dead.
And here is where the remainder of our scientific knowledge and experience come into play. We do not consider L to be a fundamental feature of the universe but a consequence of other properties. Were a technology developed that allowed for the reanimation of corpses, we need not say that a putative law of nature had been overturned; instead, we would say that the `ordinary course' had been altered by the introduction of a new yet naturalistic element. Without such technology, we expect other principles to produce L. These include thermodynamic principles. When Jesus died, there are three sorts of miraculous possibilities: either his vital tissues never fatally decayed by supernatural sustenance, his vital tissues decayed but were reconstituted gradually or suddenly prior to his reanimation, or he reanimated without the function of his vital organs. Each of these possibilities runs against other established regularities. Properly speaking, then, L is not merely the generalized rule that dead people remain dead but also the set of combinations of rules which produce that outcome. For the Resurrection to occur, every one of those combinations must fail to hold.
So a theory which advantageously counters the above independence assumption must probabilistically correlate the elements of O, have significant plausibility in its own right, and fail to assume or imply any element in L, be it the putative law itself or any combination of principles which produce that law. In this case and in the case of other miracles which violate mass/energy conservation and/or thermodynamic principles, we must toss out modern science before examining any evidence proposed against its principles. This is an absurd task, but that absurdity is consequent to proposing a suspension of the natural order.
In such a manner I tentatively maintain that the independent assumption as employed is valid in establishing an estimated upper bound on the prior odds on R. So long as we agree that it is disgustingly low, a precise value is unimportant for the strengthening of the argument. Since as you may have noticed this method of unconfirmability argument requires some detailed information concerning the relevant miracle, specifying any particular value is unimportant. For an approximate value's import to materialize, we must also delve into the category of evidence in play.
Hume appears to recognize the need for categorical bounds on the strength of evidence in his essay:
When any one tells me, that he saw a dead man restored to life, I immediately consider with myself, whether it be more probable, that this person should either deceive or be deceived, or that the fact, which he relates, should really have happened. I weigh the one miracle against the other; and according to the superiority, which I discover, I pronounce my decision, and always reject the greater miracle. If the falsehood of his testimony would be more miraculous, than the event which he relates; then, and not till then, can he pretend to command my belief or opinion. (EPHU, p.174)I think that whenever Hume attempts to place such a bound on `testimonial evidence', he overreaches by virtue of that category's broadness. "I would not believe such a story were it told to me by Cato" (p.172) does not a sufficiently general argument make, nor are vague allusions to particular failures of human reporting which remain in the background, as these do not necessarily apply to all claims that humans make. Instead, it is better to focus on more task-specific categories. It might be possible to do so, but there is no reason to argue for more than is required.
Now I must specify what I mean by a categorical bound in formal terms: roughly, a categorical bound B is a real number such whenever evidence E for an uncertain hypothesis H lies in a set C, any Bayes factor produced by E is less than or equal to B.2 That is,
If H is a miracle claim violating a putative law L supported by recaptured observations O, then tautologically the argument is successful if
What remains is to show that the evidence proposed by the miracle-claimant lies in such a set C.
What would C look like? If we want to be trivial, we can use uncontroversial examples. For example, two gamblers who have vastly differing prior odds on the fairness of a coin should not be able to resolve their dispute by tossing the coin a small number of times to check the outcomes. With precise values available, one could derive the minimum number of tosses which could possibly result in agreement.
One may extend this notion by thinking of the epistemic limitations on experiments like "tossing a coin a certain number times" as instances of methodological bounds. In the medical sciences, anecdotal and testimonial evidence as applied to broad categories of claims is almost completely useless for confirmation; careful study is required. What this reflects is a well-founded confidence in systematic errors frequently present in anecdotal reports which cannot be sufficiently discounted in the absence of controlled study. Anecdotal evidence for a novel, popular medical hypothesis cannot by nature discount those established theories and credences, a task which is necessary in order to confirm the new remedy against a significant prior implausibility.
Similar considerations apply to many classes of potential miracles and the evidence most commonly presented for them. With the Resurrection, we need not attempt the task Hume appears to set for himself in arguing that any set of witness testimony is incapable of producing convincingly calibrated Bayes factors above something like 101000. In this case, we may instead suggest that the methods of historians in establishing the historicity of those reports and their background, while possibly very good, are not so good as to allow a confident assertion that the historical record produces a Bayes factor above 101000. Myth and utter fabrication, even if wildly improbable in this case, have precedents, and I do not think they are capable of being discarded with absolute or nearly absolute confidence given the difficulties in method.
Hoping my proposals have been convincing thus far, I conclude by giving the sort of conversation which two Bayesians could have.
Christian: Ah, skeptic! Just the person I was wanting to see! I have crafted a convincing case that the Resurrection did in fact occur, and I was wanting your feedback.
Skeptic: That sounds very interesting, but before we go into the details, would you consider the Resurrection, had it occurred, to have constituted a suspension of the natural order?
Christian: Certainly, as you well know. Otherwise, the Resurrection would be meaningless. If Jesus' Resurrection were, say, a mere product of absurdly unlikely but possible quantum fluctuations, then any argument to theism or Christianity from that event would be undermined. It would be an isolated physical anomaly; nothing more, nothing less, and surely not a communicative sign of divine endorsement of the validity of Jesus' teachings.
Skeptic: I'm glad that you and I agree. And within this possibly suspended natural order, would you admit that local, epistemic generalizations hold and that tremendous confidence in those generalizations is yielded by what Hume would call `uniform sense data'?
Christian: While I obviously do not accept Hume's argument, I agree that incredulity prior to the examination of the evidence is wholly reasonable. That is why I have analyzed the evidence; one cannot say prior to analysis whether or not the evidence is sufficient or insufficient. You and I both know that this is merely a matter of probability.
Skeptic: I do not accept Hume's argument either, but one may with certain conditions be able to obviate the need to examine all of the details in advance by grounding a posteriori bounds on Bayes factors produced by certain types of evidence.
Christian: Part of this worries me, as it sounds like an excuse to avoid examining the evidence, which, as a good skeptic and Bayesian, you should be interested in doing. In any case, I suspect that such an approach would undermine important areas of scientific research, were it to be accepted.
Skeptic: I admit that this idea is a time-saver and has its ideological attractions, but allow me to specify some of those conditions. Hopefully, when you are satisfied with their stringency, your worries will vanish. But before I may do so, I nevertheless must know the nature of the argument that you are proposing. As I said before, the bounds to which I refer would be a posteriori, not some analytic consequence of Kolmogorov's axioms, uncontroversial metaphysical theses, or sound subjective Bayesian principles. I could not pretend to Hume's rhetoric and claim "an everlasting check to all kinds of superstitious delusion," or claim to have silenced any potential reasoned argument on your part or the part of your comrades in arms, be they future comrades or present confederates. In order to state exactly what I can say in advance of detailed analysis, I have to consider at least some of the details.
Christian: That at least sounds more interesting than another platitudinous regurgitation of Hume's breathless meanderings. Fine, I will play along. I am arguing, as against many prominent skeptics, to and from the historicity of the texts with respect to several key facts, especially those facts concerning the secular claims of witness testimony.
Skeptic: Have you accorded these facts certainty in your analysis as opposed to a more general analysis, for example using Jeffrey conditioning or classical conditioning on a partition of the historical possibilities?
Christian: For the facts concerning the witnesses, I strengthened the relevant arguments so as to make those facts not only plausible, but so overwhelmingly likely as to ensure that errors of omission do not seriously undermine the strength of the argument.
Skeptic: How overwhelmingly likely?
Christian: I think that I see roughly where you are heading with this. By your earlier hintings, it is clear that you are relying on some estimate of the prior odds of the Resurrection. Riddle me this: How do you propose to estimate prior odds on the Resurrection in any convincing way? You and I are both critics of equivocation and objective Bayesianism. You and I both acknowledge the limitations of current theories of calibration, especially as applied to claims like the Resurrection.
Skeptic: Properly speaking, I do no such thing.
Christian: Help me out here.
Skeptic: I rely on the notion that miracles, to occur, require a suspension of the natural order. As you have probably anticipated, I rely on the epistemic status of that natural order with respect to any potential exemption to gauge a suitable prior on the Resurrection...
Christian: Sorry to interrupt, but clearly you seem to be contradicting yourself.
Skeptic: Only if you assume that I need a specific range of prior odds. Instead, I use the deductive implications of putative laws to straightforwardly derive inequalities via the subset rule which by basic algebra translate into an upper bound on the prior odds of the Resurrection. I only need inequalities and bounds, not specific, well-defined ranges of reasonable discussion.
Christian: Ah, I see. You're assuming that the only relevant calibrating factor is the relation of a potential suspension of the natural order to the epistemic status of the natural order, of course.
Skeptic: That's right; hence why I do not claim that my approach, even if valid, would constitute the end of the discussion. One may still need to engage the evidence, but only if an adequate, well-established natural theology is formulated so as to calibrate the priors differently.
Christian: Which of course would present a serious difficulty, since the primary and standard means of evidentially filtering Christianity out of the more general category of theism is by arguing for the Resurrection. Now I am curious: supposing you could bound the prior odds on the Resurrection below 10-1000, what would you say to me if I claimed to have produced a Bayes factor based on a confidence some salient facts which is greater than 101000?
Skeptic: I would say that you have proposed the a posteriori equivalent of proving the rationality of the square root of two, Euler's number, or pi.
Christian: That's quite a strong statement; how do you mean it?
Skeptic: I might agree that your proposed facts are plausible, even extremely convincing. But I would nevertheless insist that they cannot be sufficiently plausible as to yield such a factor. Formally, I would put evidence like that you have proposed into a set of similar evidences and claim that Bayes factors in favor of the Resurrection produced by an element in that set are below 101000.
Christian: In which case, your argument would be tautological or trivial unless you can convincingly establish, before engaging all of the details, that my textual evidence cannot be stronger. Again, I do not see how you are avoiding the shortcomings of Hume.
Skeptic: Well, you have surely noted my insistence on your specifying the type of evidence in question. I doubt you fail to imagine how that might be relevant.
Christian: I have a rough idea: are you proposing theses, like those of Hume, against testimonial evidence? Just because testimonial evidence is always subject to some precedented, possible counter-thesis, that does not mean that one can say that testimonial evidence as a category must be at least this or that weak by that virtue. The details decide how significant those considerations need to be.
Skeptic: I agree, which is another reason why I do not claim to be vindicating Hume's essay. `Testimonial evidence' is perhaps too broad a category to be subject to sufficiently small, convincing categorical boundaries. As I said before, some specifics are required. Allow me to motivate those which apply to the textual record on which you plan to rely: you can envision cases where an experiment, by its nature, cannot overcome discrepancies in prior odds so as to yield agreement between two rational agents, correct?
Christian: In highly idealized scenarios like fair dice rolls or well-understood machines and programs, sure, but I do not see the relevance to a scenario so complex and multivariate as eyewitness testimony.
Skeptic: You may at least be able to anticipate a generalization of simple and uncontroversial lessons to broader notions like `historical methodology', correct?
Christian: Not exactly, as I see such a category as too vague to easily bound.
Skeptic: Again, it depends on specifics. What is the method which you used to arrive at your initial, secular factual claims? Presumably, you do not claim to have directly observed the events in question.
Christian: Of course not.
Skeptic: And so there is some significant uncertainty in the indirect inference methods, i.e. historical methods, which you employ?
Christian: At least in a trivial sense, but that need not translate into any boundary.
Skeptic: Actually, it does, unless you claim that there is no minimally significant alternative to your facts which your methods can not diminish to an arbitrary degree. For example, can you rule out as strongly as you like the possibilities of fraud and later myth-making with respect to these secular facts?
Christian: I wouldn't say that, but again, I see no reason why, in advance, I can not devalue such possibilities sufficiently as to overcome the prior implausibility of the Resurrection.
Skeptic: If by `in advance' you mean in advance of all background knowledge, surely you are correct, but I mean the reliability of your methods with respect to our current knowledge about its reliability. If that reliability is such that the probabilities of hypotheses like frauds and myths cannot be convincingly grounded below 10-1000, I have established my case. For such extreme values, I would say that this can be said further in advance than I need to argue, but to firmly secure your methods into the category which I require, I will need to know a few more specifics.
Christian: I think I understand now, and I think that I see how you will be able to secure your conclusions were I to spell out more details. I suppose that I will have to qualify my paper with a placeholder for the time being and play with the formalisms to double-check your statements.
Skeptic: That sounds fine. In the meantime, I would be happy to read your paper. After all, you might be able to calibrate the relevant priors differently. It is still worth reading, for this and other reasons, if your conclusions are as strongly supported as you have suggested.
Christian: I look forward to your review. However, I hope you only resume technical blogging after all that wine you just drank leaves your system.
Skeptic: You're breaking the fourth wall.
1. The simplifying assumption of equal-weightedness is not generally true. If alternatives to the law include something like `dead people remain dead unless you perform a certain magic ritual', then only failures of that ritual will contrast the hypothesis with L. We can recapture the plausibility of the assumption by stipulating that a theoretical agent at this theoretical threshold point has effectively ruled any particular such hypothesis.
2. I've been playing with this notion for some time, and I know of several generalizations if anyone is interested.
Hume and the confirmability of miracles
While discussing the McGrews' Bayesian analysis of the Resurrection (CCRJ), I frequently mentioned that the McGrews and myself were not attempting to derive odds on the Resurrection. Rather, we were focusing on the Bayes factor - aka the likelihood ratio - which if you recall, is the number by which the prior odds ratio p(`thing')/p(`other thing') is multiplied to yield the posterior odds ratio q(`thing')/q(`other thing'). So at the very minimum, one needs to estimate what the prior odds should be in order to derive the final odds. Since neither of our approaches were sufficiently general to capture a truly cumulative Bayes factor, even this may be inadequate, but since the factor I derived - 106 - was calibrated given generous textual assumptions in favor of the Resurrection, we may be able to tentatively estimate an upper bound on reasonable posterior odds using that factor if we have an upper bound on reasonable priors. If that upper bound is less than 10-6, we may conclude that the Resurrection probably did not occur, i.e. 0.5>q(R).
I opine that barring other arguments in the context of a natural theology, such an upper bound exists. That is, the Resurrection can not reasonably be confirmed from the textual record alone with respect to convincing background knowledge which is shared by skeptics and Christians alike. But I am interested in Hume's more general thesis, which is that miracles by their nature can not reasonably be confirmed. The details of an analysis of the Resurrection are merely an instance of a more general unconfirmability argument.
I pause to obviate a potential objection: I am fully aware that the proper interpretation of Hume's Enquiry concerning Human Understanding, especially Of Miracles, is a hotly disputed topic. I am attributing an unconfirmability argument to Hume; I doubt he can be convincingly interpreted as not making such an argument. But I am not here interested in any historical exoneration or conviction of Hume of philosophical crimes. Rather, I want to work with his apparent argument by recasting it in formal terms, propose that it is inadequate, and attempt to shape a more satisfactory unconfirmability argument.
I am neither discussing nor proposing a definition-dependent impossibility argument, e.g., "A miracle is the violation of mathematical, divine, immutable, eternal laws. By the very exposition itself, a miracle is a contradiction in terms: a law cannot at the same time be immutable and violated." Rather, I am interested in miracles loosely defined as particular exceptions to otherwise exceptionless laws or regularities of nature. In this context, the regularities of importance are putative laws, and their importance is epistemic, not ontological. Whether or not a putative law is true is largely irrelevant: what matters is how well-supported it is.
The proper definition of a miracle is also in dispute. As regards this item, I follow Tim and Lydia McGrew in treating the Resurrection as a paradigm (CCRJ, p.4). As I will explain in the course of this discussion, working with paradigm cases like the Resurrection is all that should be required. Failures of consensus on miracles are relevant to Hume's argument, but they will not prove necessary to reject his conclusion. Which is roughly as follows:
Hume's Argument: There cannot exist evidence E for a miracle M such that
.
With conditionalization, this is equivalent to stating that the posterior odds on a miracle can never be greater than 1/2.1
The initial prospects of this statement are rather dim. As is commonly pointed out, there are no a priori boundaries on the size of Bayes factors: no matter how small the prior odds on a miracle, there exist finite Bayes factors which can overcome them. Similarly, disputes concerning the definition of a miracle make it impossible to have confidence in such a general statement.
I would also add that we should not be overly interested in such an argument as employed to justify ignoring any potential evidence for miracles. The debate is worthwhile. As I have noted in a slightly different context:
I will not second another common objection: I do not think that Hume's argument, interpreted as I have interpreted it, would destroy the possibility of overturning laws in science. His "straight rule of induction" is problematic in this context (Earman, pp.31-2), but laws are not to my knowledge overturned in the way that a putative miracle claim would overturn them.
Take the Conservation of Mass. Did measurements of nuclear reactions overturn a uniform experience? No, because what changed was not the article where uniform experience applied, but where a novelty was being analyzed. If for example I react 50 grams of sodium with 70 grams of chlorine gas to form salt (NaCl) at approximately standard temperature and pressure and measure a net change in mass of 20 grams, I or my instruments screwed up. Mass is still conserved within significant margins of instrumental error for `ordinary' chemical reactions. The implications of such experience have not been contradicted, but superseded. With miracles, where the putative law needs to otherwise be intact for theological reasons, no such consideration applies. We are not talking supercessions or the overturning of laws as done in the sciences; we are talking about flat-out, singular violations of an otherwise sound natural order. We are talking about an experiment incapable of replication. Were mass conservation to always hold, and the only exception were to occur in one apparently sound experiment, we should have discounted the experiment as flawed if replication failed.
I judge Hume's argument to be a failure and its conclusion to be unsound. But this need not be the end of the story. We may yet build a better monument by clearing away the noisy rubble of Hume's rhetoric and picking out the useful pieces. That will be the subject of my next post.
1. This interpretation, though disputed, has a lot of support, perhaps apart from the target threshold 0.5>q(M). Were Hume making an impossibility argument, it is odd that he should emphasize the relative strength of evidences (p.169) and the uncertainty of the relevant propositions (pp.169-70); that he discusses evidence at all would also be strange. In addition to his use of probabilistic terminology, he also casts his argument in terms of degrees-of-confidence: "Some events are found, in all countries and all ages, to have been constantly conjoined together: Others are found to have been more variable, and sometimes to disappoint our expectations; so that, in our reasonings concerning matter of fact, there are all imaginable degrees of assurance, from the highest certainty to the lowest species of moral evidence." And he continues famously: "A wise man, therefore, proportions his belief to the evidence. In such conclusions as are founded on an infallible experience, he expects the event with the last degree of assurance, and regards his past experience as a full proof of the future existence of that event" (p.170).
With terms like `infallible' and `proof' in play, I think that Hume may be interpreted as arguing for a prior probability of zero for miracles, or perhaps an infinitesimal probability (p.171). But I do not think that such a prior is convincing to all - or many - concerned, and it is therefore useless. Many Bayesians accept - here the terminology is unfortunate - the principle of regularity, which states that all possibilities have probability greater than 0, assuming that those possibilities are uncertain and assigned any probability whatever. In any case, we are presumably inviting Christians to the discussion, so we must at least assume that non-zero priors are in play.
There are other ambiguities, and I am lead to second Earman's hostile conclusion (p.20):
I opine that barring other arguments in the context of a natural theology, such an upper bound exists. That is, the Resurrection can not reasonably be confirmed from the textual record alone with respect to convincing background knowledge which is shared by skeptics and Christians alike. But I am interested in Hume's more general thesis, which is that miracles by their nature can not reasonably be confirmed. The details of an analysis of the Resurrection are merely an instance of a more general unconfirmability argument.
I pause to obviate a potential objection: I am fully aware that the proper interpretation of Hume's Enquiry concerning Human Understanding, especially Of Miracles, is a hotly disputed topic. I am attributing an unconfirmability argument to Hume; I doubt he can be convincingly interpreted as not making such an argument. But I am not here interested in any historical exoneration or conviction of Hume of philosophical crimes. Rather, I want to work with his apparent argument by recasting it in formal terms, propose that it is inadequate, and attempt to shape a more satisfactory unconfirmability argument.
I am neither discussing nor proposing a definition-dependent impossibility argument, e.g., "A miracle is the violation of mathematical, divine, immutable, eternal laws. By the very exposition itself, a miracle is a contradiction in terms: a law cannot at the same time be immutable and violated." Rather, I am interested in miracles loosely defined as particular exceptions to otherwise exceptionless laws or regularities of nature. In this context, the regularities of importance are putative laws, and their importance is epistemic, not ontological. Whether or not a putative law is true is largely irrelevant: what matters is how well-supported it is.
The proper definition of a miracle is also in dispute. As regards this item, I follow Tim and Lydia McGrew in treating the Resurrection as a paradigm (CCRJ, p.4). As I will explain in the course of this discussion, working with paradigm cases like the Resurrection is all that should be required. Failures of consensus on miracles are relevant to Hume's argument, but they will not prove necessary to reject his conclusion. Which is roughly as follows:
Hume's Argument: There cannot exist evidence E for a miracle M such that
With conditionalization, this is equivalent to stating that the posterior odds on a miracle can never be greater than 1/2.1
The initial prospects of this statement are rather dim. As is commonly pointed out, there are no a priori boundaries on the size of Bayes factors: no matter how small the prior odds on a miracle, there exist finite Bayes factors which can overcome them. Similarly, disputes concerning the definition of a miracle make it impossible to have confidence in such a general statement.
I would also add that we should not be overly interested in such an argument as employed to justify ignoring any potential evidence for miracles. The debate is worthwhile. As I have noted in a slightly different context:
It is very often said, by e.g. PZ Myers and Massimo Pigliucci, that one cannot evidence Christianity or gods because they are not coherent hypotheses. More needs to be said about this, but I would at least suggest the following: if the evidence for the Resurrection really is extremely convincing to reasonable people on the assumption of coherency, we should take an attitude similar to that which I think we take to science: some conceptual fuzziness is to be tolerated, barring flat contradiction, where overwhelming evidence for an aspect of a theory is available. Were I to find the evidence for the Resurrection convincing, I know I would be working very diligently to craft a coherent Christian philosophy to accommodate it. So to me, the coherency difficulty is in many ways secondary, unless that difficulty is so severe that one cannot even begin to discuss relevant evidence. I think we usually manage to do so. Wouldn't you agree?The argument also conflicts with the empirical, tentative nature of skeptical inquiry. I think we should wish to avoid such categorical statements.
The temptation to fashion such an argument is understandable. But it should be resisted. Any epistemology that does not allow for the possibility that evidence, whether from eyewitness testimony or from some other source, can establish the credibility of a UFO landing, a walking on water, or a resurrection is inadequate. (Earman, p.4)As Earman also notes, there are events which, were they to occur, surely amount to convincing evidence for a miracle claim:
Suppose, for the sake of illustration, that there is a well developed theology based on the existence of a god called Emuh. who promises an afterlife in return for certain religious observances in this life. Suppose that this theology predicts that on such-and-such a day Emuh will send a sign in the sky. And suppose that on the appointed day, the clouds over America clearly spell out in English the words “Believe in Emuh and you will have everlasting life,” while the same message is spelled out in French over France, in Deutsch over Germany, etc. Then even though these cloud formations may not contravene any of the general principles taken at the time in question to be laws of nature and, indeed, may be explicable in terms of those principles, it would not be untoward to take these extraordinary occurrences to be support for Emuh theology. (p.11)So Hume's argument, were it valid and coherent, would prove too much. It also ignores the effect of evidence for a theology and its implications for the proposed miracle claim. Were the gloating fiction of LaHaye's Left Behind series to be actualized, it would confirm the Resurrection. I am unsure as to how or why someone would seriously argue otherwise, even if the various details of Christian theology are unclear.
I will not second another common objection: I do not think that Hume's argument, interpreted as I have interpreted it, would destroy the possibility of overturning laws in science. His "straight rule of induction" is problematic in this context (Earman, pp.31-2), but laws are not to my knowledge overturned in the way that a putative miracle claim would overturn them.
Take the Conservation of Mass. Did measurements of nuclear reactions overturn a uniform experience? No, because what changed was not the article where uniform experience applied, but where a novelty was being analyzed. If for example I react 50 grams of sodium with 70 grams of chlorine gas to form salt (NaCl) at approximately standard temperature and pressure and measure a net change in mass of 20 grams, I or my instruments screwed up. Mass is still conserved within significant margins of instrumental error for `ordinary' chemical reactions. The implications of such experience have not been contradicted, but superseded. With miracles, where the putative law needs to otherwise be intact for theological reasons, no such consideration applies. We are not talking supercessions or the overturning of laws as done in the sciences; we are talking about flat-out, singular violations of an otherwise sound natural order. We are talking about an experiment incapable of replication. Were mass conservation to always hold, and the only exception were to occur in one apparently sound experiment, we should have discounted the experiment as flawed if replication failed.
I judge Hume's argument to be a failure and its conclusion to be unsound. But this need not be the end of the story. We may yet build a better monument by clearing away the noisy rubble of Hume's rhetoric and picking out the useful pieces. That will be the subject of my next post.
1. This interpretation, though disputed, has a lot of support, perhaps apart from the target threshold 0.5>q(M). Were Hume making an impossibility argument, it is odd that he should emphasize the relative strength of evidences (p.169) and the uncertainty of the relevant propositions (pp.169-70); that he discusses evidence at all would also be strange. In addition to his use of probabilistic terminology, he also casts his argument in terms of degrees-of-confidence: "Some events are found, in all countries and all ages, to have been constantly conjoined together: Others are found to have been more variable, and sometimes to disappoint our expectations; so that, in our reasonings concerning matter of fact, there are all imaginable degrees of assurance, from the highest certainty to the lowest species of moral evidence." And he continues famously: "A wise man, therefore, proportions his belief to the evidence. In such conclusions as are founded on an infallible experience, he expects the event with the last degree of assurance, and regards his past experience as a full proof of the future existence of that event" (p.170).
With terms like `infallible' and `proof' in play, I think that Hume may be interpreted as arguing for a prior probability of zero for miracles, or perhaps an infinitesimal probability (p.171). But I do not think that such a prior is convincing to all - or many - concerned, and it is therefore useless. Many Bayesians accept - here the terminology is unfortunate - the principle of regularity, which states that all possibilities have probability greater than 0, assuming that those possibilities are uncertain and assigned any probability whatever. In any case, we are presumably inviting Christians to the discussion, so we must at least assume that non-zero priors are in play.
There are other ambiguities, and I am lead to second Earman's hostile conclusion (p.20):
I defy the reader to give a short, simple, and accurate summary of the argumentation in "Of Miracles." What on first reading appears to be a seamless argument is actually a collection of considerations that sometimes mesh and sometimes don't. It will take much work to tease out the components of Hume's argument and to evaluate the soundness of individual components and the effectiveness of the entire package.Immediately after bringing up `proofs' of experience, Hume dives right back into emphasizing the fallibility of evidence, particularly witness testimony (EPHU, p.171). There are other deficiencies in his presentation. After defining miracles as putative exceptions to uniformly evidenced laws, he states the following:
There must, therefore, be a uniform experience against every miraculous event, otherwise the event would not merit that appelation. And as a uniform experience amounts to a proof, there is here a direct and full proof, from the nature of the fact, against the existence of any miracle; nor can such a proof be destroyed, or the miracle rendered credible, but by an opposite proof, which is superior. (p.173)With this stringency, the mere proposal of evidence for an event disqualifies that event's being a miracle, as experience is no longer uniformly against it. And then, the presentation of additional evidence should leave an opening. I'll stick with the Bayesian interpretation because it is the only plausible interpretation to be found.
Friday, July 15, 2011
A Primer on Bayesian Philosophy: 2 - Bayesianism outlined
Bayesianism is broader than probabilism, the idea that credence can be represented by a function satisfying basic probability axioms. Accepting probabilism, many important questions are left open. Most importantly, how are scientific theories confirmed? How should new information affect our commitments? How do we contrast competing theories?
New evidence should lead to a new probability function; the problem is how to relate old probabilities to new probabilities. That is, what is the posterior probability of a hypothesis given the prior probability of the hypothesis and an update in the probability of some evidence?
Suppose that you observe the occurrence of a previously uncertain event E. Denote your prior probability by p and your posterior by q, so that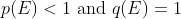
.
Simple Conditionalization.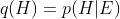
.
Updating on E, your posterior credence of H is your prior conditional of H given E. Further, those conditionals do not change. This is equivalent to assuming that odds ratios are invariant, i.e.
}{q(H^c)}=\frac{p(H)}{p(H^c)} "\frac{q(H)}{q(H^c)}=\frac{p(H)}{p(H^c)}")
In English, to deny conditionalization is to claim that absolute odds - odds which ignore the updated evidence - change.
Rigidity. For arbitrary events A and B,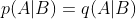
.
Before discussing the shortcomings and limitations of these principles, it is worth seeing what they can do for us. Some of you may be aware of the hypothetico-deductive model of science; the hypothetico-deductive principle follows from probabilism, conditionalization, and rigidity.
(I pause to say that this is really freakin' cool, and what follows was sufficient to provoke further study when I was introduced to it by a professor.)
Hypothetico-deductive principle. Let p be a prior probability, H denote an uncertain hypothesis, and E be uncertain evidence. If H is p-positively relevant to E - that is, p(H|E)>p(H), or equivalently by Bayes' theorem, p(E|H)>p(E) - and q(E)=1, then q(H)>p(H).
Proof. By conditionalization,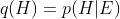. By Bayes' theorem, 
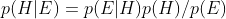. Since 
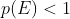, we have 
. By \leq1 "p(E|H)\leq1")
and rigidity, the result follows.
Short, sweet, and really really cool. If some theory makes a large number of uncertain predictions which are subsequently verified, the probability of the theory will approach one with reasonable assumptions. More properly, such observations impose very strong restrictions on posterior probabilities which fail to give high probability to a theory.
This principle can be stated more strongly: we may also determine the strength of confirmation yielded by evidence using Bayes' theorem. Recall the odds form of Bayes' theorem:
}{p(H^c|E)}=\frac{p(E|H)}{p(E|H^c)}\times\frac{p(H)}{p(H^c)} "\frac{p(H|E)}{p(H^c|E)}=\frac{p(E|H)}{p(E|H^c)}\times\frac{p(H)}{p(H^c)}")
As promised, rigidity and conditionalization justify the terminologies `posterior odds' and `prior odds'. Note that the Bayes factor
}{p(E|H^c)} "\beta=\frac{p(E|H)}{p(E|H^c)}")
is the number by which the prior odds is multiplied to yield the posterior odds. If E is p-positively relevant to H, this number is greater than 1, and vice-versa. This number may be thought of as quantifying the strength of confirmation of H yielded by E.
That's obviously a very useful concept. It can be used to resolve paradoxes of confirmation which result from fairly simple assumptions like Nicod's Criterion, which states that observations of a previously uncertain particular instance confirm the corresponding regularity, if uncertain. This and logical equivalence entail that observing a non-black non-raven increases the probability of `all ravens are black'. The usual Bayesian response is to accept this counter-intuitive implication and explain why it is unproblematic by justifying the employment of differing Bayes factors. Observing a green apple confirms that all ravens are black, but not nearly so much as observing a black raven. And the uses are not limited to theoretical concerns; the practical utility of Bayes' theorem is overwhelming. Here, I'll let e-jedis provide the examples.1
So far, I have only presented the odds form of Bayes theorem to contrast a hypothesis and its complement, but the equation is the same for any two uncertain hypotheses. But you could fairly ask whether or not conditionalization as I have presented it is too simple. Can we update on uncertain evidence, i.e. when 1>q(E)?
Here the works of the late Richard Jeffrey are indispensable.2 Jeffrey Conditioning, or probability kinematics, is the standard way of updating probabilities in light of uncertain evidence. I opine that such a method is essential; as Jeffrey states: "Certainty is quite demanding. It rules out not only the far-fetched uncertainties associated with philosophical skepticism, but also the familiar uncertainties that affect real empirical inquiry in science and everyday life" (Subjective Probability, p.57).
Probability Kinematics. Let your prior probability be p and your posterior probability be q. Then if
is a partition of the sample space where q(E_i)>0 for all i,
=\sum_{i\in[n]}p(H|E_i)q(E_i) "q(H)=\sum_{i\in[n]}p(H|E_i)q(E_i)")
Note that this follows from rigidity and simple conditionalization with 1>q(E). Simple/classic conditioning is the case that one block in this partition, E, is treated as certain.
Ok, so we know that Bayesian confirmation is theoretically and practically useful for resolving extremely broad classes of problems. But what are some of the problems and limitations with the theory?
Many of the issues concern assigning prior odds, interpretations of probability, and defending Bayesianism against other theories of credence; these will have to wait for the next two sections. A key limitation is that Bayesian learning cannot account for all learning. It requires logical omniscience: If you discover a logical implication, you must rework your prior accordingly. It requires rigidity: if you find out that your prior conditional probability was poorly calibrated - say due to inadequate statistical data - you have to redo the assessment. The domain of your prior may also be inadequate; the consideration of previously unimagined events and expectations must be included in a reworking. But these are merely the shortcomings of us mortal practitioners; what about theoretical shortcomings?
Normalizability is an issue: one cannot assign non-zero probabilities to uncountably many disjoint propositions. As most would agree that there is such a class of propositions, probability can never be complete, as uncountable sums of positive numbers always diverge.3 Everything discussed so far has also assumed that probabilities are particular real numbers. The theory must be expanded to account for vague probabilities.
These warnings mentioned, we can move on to the standard defense of Bayesianism.
1. This link is highly highly recommended, as is a related link by the same author.
2. I recommend reading his Subjective Probability: The Real Thing, a delightfully concise account which also includes a probability primer, many illustrative examples, and lots of exercises.
3. This issue is explored in detail in Hájek's What Conditional Probability Could not Be, amongst other places. For example, one cannot assign a probability to propositions about infinitely fine darts landing on particular points in a continuous region. Here many have sought to introduce infinitesimals to generalize probability - Hájek also discusses this - but such accounts run into fatal problems, and their prospects are dim.
New evidence should lead to a new probability function; the problem is how to relate old probabilities to new probabilities. That is, what is the posterior probability of a hypothesis given the prior probability of the hypothesis and an update in the probability of some evidence?
Suppose that you observe the occurrence of a previously uncertain event E. Denote your prior probability by p and your posterior by q, so that
Simple Conditionalization.
Updating on E, your posterior credence of H is your prior conditional of H given E. Further, those conditionals do not change. This is equivalent to assuming that odds ratios are invariant, i.e.
In English, to deny conditionalization is to claim that absolute odds - odds which ignore the updated evidence - change.
Rigidity. For arbitrary events A and B,
Before discussing the shortcomings and limitations of these principles, it is worth seeing what they can do for us. Some of you may be aware of the hypothetico-deductive model of science; the hypothetico-deductive principle follows from probabilism, conditionalization, and rigidity.
(I pause to say that this is really freakin' cool, and what follows was sufficient to provoke further study when I was introduced to it by a professor.)
Hypothetico-deductive principle. Let p be a prior probability, H denote an uncertain hypothesis, and E be uncertain evidence. If H is p-positively relevant to E - that is, p(H|E)>p(H), or equivalently by Bayes' theorem, p(E|H)>p(E) - and q(E)=1, then q(H)>p(H).
Proof. By conditionalization,
Short, sweet, and really really cool. If some theory makes a large number of uncertain predictions which are subsequently verified, the probability of the theory will approach one with reasonable assumptions. More properly, such observations impose very strong restrictions on posterior probabilities which fail to give high probability to a theory.
This principle can be stated more strongly: we may also determine the strength of confirmation yielded by evidence using Bayes' theorem. Recall the odds form of Bayes' theorem:
As promised, rigidity and conditionalization justify the terminologies `posterior odds' and `prior odds'. Note that the Bayes factor
is the number by which the prior odds is multiplied to yield the posterior odds. If E is p-positively relevant to H, this number is greater than 1, and vice-versa. This number may be thought of as quantifying the strength of confirmation of H yielded by E.
That's obviously a very useful concept. It can be used to resolve paradoxes of confirmation which result from fairly simple assumptions like Nicod's Criterion, which states that observations of a previously uncertain particular instance confirm the corresponding regularity, if uncertain. This and logical equivalence entail that observing a non-black non-raven increases the probability of `all ravens are black'. The usual Bayesian response is to accept this counter-intuitive implication and explain why it is unproblematic by justifying the employment of differing Bayes factors. Observing a green apple confirms that all ravens are black, but not nearly so much as observing a black raven. And the uses are not limited to theoretical concerns; the practical utility of Bayes' theorem is overwhelming. Here, I'll let e-jedis provide the examples.1
So far, I have only presented the odds form of Bayes theorem to contrast a hypothesis and its complement, but the equation is the same for any two uncertain hypotheses. But you could fairly ask whether or not conditionalization as I have presented it is too simple. Can we update on uncertain evidence, i.e. when 1>q(E)?
Here the works of the late Richard Jeffrey are indispensable.2 Jeffrey Conditioning, or probability kinematics, is the standard way of updating probabilities in light of uncertain evidence. I opine that such a method is essential; as Jeffrey states: "Certainty is quite demanding. It rules out not only the far-fetched uncertainties associated with philosophical skepticism, but also the familiar uncertainties that affect real empirical inquiry in science and everyday life" (Subjective Probability, p.57).
Probability Kinematics. Let your prior probability be p and your posterior probability be q. Then if
Note that this follows from rigidity and simple conditionalization with 1>q(E). Simple/classic conditioning is the case that one block in this partition, E, is treated as certain.
Ok, so we know that Bayesian confirmation is theoretically and practically useful for resolving extremely broad classes of problems. But what are some of the problems and limitations with the theory?
Many of the issues concern assigning prior odds, interpretations of probability, and defending Bayesianism against other theories of credence; these will have to wait for the next two sections. A key limitation is that Bayesian learning cannot account for all learning. It requires logical omniscience: If you discover a logical implication, you must rework your prior accordingly. It requires rigidity: if you find out that your prior conditional probability was poorly calibrated - say due to inadequate statistical data - you have to redo the assessment. The domain of your prior may also be inadequate; the consideration of previously unimagined events and expectations must be included in a reworking. But these are merely the shortcomings of us mortal practitioners; what about theoretical shortcomings?
Normalizability is an issue: one cannot assign non-zero probabilities to uncountably many disjoint propositions. As most would agree that there is such a class of propositions, probability can never be complete, as uncountable sums of positive numbers always diverge.3 Everything discussed so far has also assumed that probabilities are particular real numbers. The theory must be expanded to account for vague probabilities.
These warnings mentioned, we can move on to the standard defense of Bayesianism.
1. This link is highly highly recommended, as is a related link by the same author.
2. I recommend reading his Subjective Probability: The Real Thing, a delightfully concise account which also includes a probability primer, many illustrative examples, and lots of exercises.
3. This issue is explored in detail in Hájek's What Conditional Probability Could not Be, amongst other places. For example, one cannot assign a probability to propositions about infinitely fine darts landing on particular points in a continuous region. Here many have sought to introduce infinitesimals to generalize probability - Hájek also discusses this - but such accounts run into fatal problems, and their prospects are dim.
A Primer on Bayesian Philosophy: 4- Interpretation and Subjectivity (part 2)
A brief summary is in order. The roughly common ground in the following post is that rational agents assign credences which obey the probability calculus (probabilism) and update probabilities using Bayes' theorem (conditionalization). Means of constraining `reasonable' probabilities using evidence are not universal, but some heuristics are accepted (calibration). The conjunction of these items is a decent description of empirical subjective Bayesianism, referred to simply as subjective Bayesianism.
There are two areas of dispute which characterize objective Bayesianism. The first is degree of calibration, and the second is equivocation.1 As far as I am aware, there is no clear consensus concerning the former; the category is rather soft. The more important dispute concerns equivocation.
There are two applications of equivocation: that which is applied in the absence of relevant evidence and that which is applied after calibration. This are features of the same rule, but the problems feel a little different. Equivocation, as applied in the absence of calibrating evidence, is the principle of indifference a.k.a. the principle of insufficient reason. You list your N (atomic) possibilities and assign each one a probability of 1/N (the discrete uniform distribution). If there the sample space is infinite, you assign the continuous uniform distribution.
The main problem is the most obvious. The goal of equivocation is to ascribe `informationless' priors in order to avoid unjustified prejudice for or against propositions in the absence of evidence.2 The uniform distribution is not an assumption, but is itself a result of assuming that one knows nothing about the distribution (!). (One derives this by comparing the unknown distribution to a null data set.) But admirable as this might seem, the results are absurd.
The underlying problem is that equivocation depends on partition choice, the way in which the possibilities are enumerated. For a common and more devastating example, suppose that you are told that a square fence with side length between 10 feet and 20 feet is being constructed. By equivocation, you should assign prob(`side length is below 15 feet')=1/2. But the question is logically equivalent to the following: what is the probability that the area enclosed by a square fence is below 225 given that the area is between 100 and 400 feet squared? Equivocating, you should say that it is (225-100)/(400-100)=125/300. Oddly enough, the `informationless prior' depends on how the question is formulated. Modern reformulations of equivocation, including MaxEnt, run into similar problems.
So an equivocation norm would in fact prejudice us against certain possibilities and deems certain agents unreasonable on a priori grounds. The Principle of Indifference and MaxEnt have their uses, but these are subsumed within the more general subjective account.
There is of course much more to this dispute. Readers may consult Howson and Urbach (1989) and Williamson (2010) for details, but some further overview is provided by Elliott Sober in Bayesianism -- Its Scope and Limits.
1. See section F in the SEP article. Note also that Williamson and others do not accept general conditionalization.
2. See (Howson and Urbach, pp.45-54) for a discussion.
There are two areas of dispute which characterize objective Bayesianism. The first is degree of calibration, and the second is equivocation.1 As far as I am aware, there is no clear consensus concerning the former; the category is rather soft. The more important dispute concerns equivocation.
There are two applications of equivocation: that which is applied in the absence of relevant evidence and that which is applied after calibration. This are features of the same rule, but the problems feel a little different. Equivocation, as applied in the absence of calibrating evidence, is the principle of indifference a.k.a. the principle of insufficient reason. You list your N (atomic) possibilities and assign each one a probability of 1/N (the discrete uniform distribution). If there the sample space is infinite, you assign the continuous uniform distribution.
The main problem is the most obvious. The goal of equivocation is to ascribe `informationless' priors in order to avoid unjustified prejudice for or against propositions in the absence of evidence.2 The uniform distribution is not an assumption, but is itself a result of assuming that one knows nothing about the distribution (!). (One derives this by comparing the unknown distribution to a null data set.) But admirable as this might seem, the results are absurd.
Suppose that you draw a ball from an urn which you are told contains white and coloured balls in some unknown proportion, and that the coloured balls are either red or blue. What sort of ball will you draw? Your data seem to be neutral, in the first instance, between its being white or coloured. Hence according to the Principle of Indifference, the probability that it will be white is one half But if it is coloured, the ball is red or blue, and the data are surely neutral between the ball's being either white or blue or red. Hence according to the Principle of Indifference, the probability of the ball's being white is one third (Howson and Urbach, p.45).
The underlying problem is that equivocation depends on partition choice, the way in which the possibilities are enumerated. For a common and more devastating example, suppose that you are told that a square fence with side length between 10 feet and 20 feet is being constructed. By equivocation, you should assign prob(`side length is below 15 feet')=1/2. But the question is logically equivalent to the following: what is the probability that the area enclosed by a square fence is below 225 given that the area is between 100 and 400 feet squared? Equivocating, you should say that it is (225-100)/(400-100)=125/300. Oddly enough, the `informationless prior' depends on how the question is formulated. Modern reformulations of equivocation, including MaxEnt, run into similar problems.
So an equivocation norm would in fact prejudice us against certain possibilities and deems certain agents unreasonable on a priori grounds. The Principle of Indifference and MaxEnt have their uses, but these are subsumed within the more general subjective account.
There is of course much more to this dispute. Readers may consult Howson and Urbach (1989) and Williamson (2010) for details, but some further overview is provided by Elliott Sober in Bayesianism -- Its Scope and Limits.
1. See section F in the SEP article. Note also that Williamson and others do not accept general conditionalization.
2. See (Howson and Urbach, pp.45-54) for a discussion.
A Primer on Bayesian Philosophy: 3 - Arguments
So far, Bayesianism has been introduced as the conjunction of probabilism and a confirmation theory. But why should credence obey the probability axioms?
Bayesianism is usually defended by Dutch book arguments. However, these arguments are not based on empirical observation or on deduction from widely-shared premises; what then might they be, exactly?
Since the character of a Dutch book is not empirical, it is often - and I think correctly - admitted that Bayesian rationality is not binding on all `rational' persons in the normal sense of the term.1 Argumentation in these matters is largely limited to finding intuitive and pragmatic desiderata and comparing differing accounts under a plausible interpretation. Wager interpretations, in which probabilities represent the value at which one is willing to bet for/against the occurrence of a proposition, are very common. And it is on such an interpretation conjoined with an idea of what a `wise better' should do that Dutch books are based. Probabilism, conditionalization, and probability kinematics all have Dutch book defenses. In literal terms, you make sure that your credences are probabilities to avoid making stupid bets. Agents who obey the probability norms are said to be coherent, and this is the minimal standard of Bayesian rationality.3
Before going further, I'll give my own amateur opinion - though one many of my superiors share if I judge correctly - on argumentation about Bayesianism. To me, the key defense of Bayesianism is Carnapian; it is a very powerful and readily comprehensible tool. Even if I thought Dutch books complete and miserable failures, I would still be writing these posts. To me, this post is inessential, and I would be entirely uninjured were readers to skip this information. But Dutch books are really interesting, and if you read further, you will run into them. So I should introduce them regardless of whether I deem them inessential, but I am also happy to introduce them for their own sake.2
I think my intuitions about Bayesianism are well-founded. It seems strange to not have a minimal credence, i.e. 0, which applies to necessary falsehoods. I do not think it is sensible to say "I am less committed to an uncertain proposition than I am a necessary falsehood." Similarly, I think it nonsensical to lack a maximum value of commitment: try to imagine committing to an uncertain proposition more strongly than you do a tautology. That credence is one-dimensional and continuous is more difficult; the latter of which is mostly an item of computational convenience, just as continuity in physics is. As Carnap mentions - and I'll trust his knowledge of the physics - our measurements of the world are entirely compatible with strictly rational-valued spacial coordinates, but the loss of continuity would present absurd and unnecessary difficulties in calculation and theory. For one-dimensionality, I think one should always be able to say of two propositions that credence may be compared, i.e. the ordering should be complete as it is on the real numbers. So vector-valued credences should have a real norm. If it is e.g. the max norm, then multi-dimensionality adds no effect. If it is e.g. the standard Euclidean norm on 2-dimensional real vectors, then tautologies would having (1) different credences - the points would lie somewhere on the unit circle in the first quadrant - or (2) the same credence, e.g. "(1/\sqrt{2},1/\sqrt{2})")
. In this case, credences lie on line between  "(0,0)")
and , in which case we are back to one-dimensionality, or on a different line, in which case uncertain propositions may be said to be `more certain in one respect' than a tautology. So in cases (1) and (2), we are forced to make distinctions in the credence assigned to different tautologies. I do not see any value in such an approach, nor any immediate need for it.
A case of finite additivity - the complement rule - is also intuitive; try saying that you believe in a proposition with 50% confidence and you believe in its negation with a confidence other than 50%. But additivity generally is more difficult to defend with intuitions and pragmatism, and it does the computational work in probability theory. Why should the disjunction of contradictory hypotheses have additive credence?
There is an intuitive, geometric way of looking at this. Picture a normalized Venn diagram, say a unit square or circle. Then the region represented by two disjoint propositions is disconnected within that diagram; (at least) two sub-regions are non-overlapping, e.g. this. Then the sum of the total area is the sum of the disjoint sub-regions. Similarly, when two regions overlap, the `correct' formula for the total area is given by the inclusion/exclusion principle. Additivity also allows us to `slice up' such a diagram (a partition) and not worry about a failure of normalization.
I think that such considerations and the successful application of probability theory in the sciences are sufficient for a cautious acceptance and application of Bayesianism. I am not saying that it is the only appropriate method for credences. I do not think for example that one should always avoid vague probability; I will discuss how Bayesians can deal with vagueness later. But up to assigning particular values, I have found Bayesian credence more than satisfactory. That all said, I can talk about Dutch books.
I'll be lazy and borrow from the SEP supplement:
As mentioned before, the colloquial Dutch book argument is `make probabilistic bets or risk a guaranteed loss', but I agree with the SEP article that Dutch book arguments are claims about pragmatic self-defeat in light of the objections and qualifications. In the context of science, we want to avoid distributing our credences in a way that could ensure inaccuracy. (I assume that nature is not a kindly bookie.)
But if violating the probability axioms could ensure defeat, could it not also ensure victory? Yes, as it turns out, and such an eventuality is called a `Czech book' by Hájek: ``Iff you violate probability theory, there exists a specific bad thing (a Dutch Book against you). Iff you violate probability theory, there exists a specific good thing (a Czech Book for you) (p.797). Hájek explores ways of preserving the Dutch Book - I think with success, along with a few other arguments in the article.
I'll leave the interested reader there.4
1. See e.g. (Howson and Urbach, p.75).
2. This section is a quick read, as is the supplement, to give you some idea of what these arguments look like.
3. This standard is very lax. To use a shopworn illustration, a person who believes that the moon is made of cheese with 90% confidence is `rational' in this sense so long as he believes the moon is NOT made of cheese with 10% confidence. Probabilistic accounts of `reasonableness' will be discussed elsewhere.
4. In case the link breaks, the Hájek's article is Arguments for - or against - probabilism? and is readily accessible in several locations via a Google search.
Bayesianism is usually defended by Dutch book arguments. However, these arguments are not based on empirical observation or on deduction from widely-shared premises; what then might they be, exactly?
Since the character of a Dutch book is not empirical, it is often - and I think correctly - admitted that Bayesian rationality is not binding on all `rational' persons in the normal sense of the term.1 Argumentation in these matters is largely limited to finding intuitive and pragmatic desiderata and comparing differing accounts under a plausible interpretation. Wager interpretations, in which probabilities represent the value at which one is willing to bet for/against the occurrence of a proposition, are very common. And it is on such an interpretation conjoined with an idea of what a `wise better' should do that Dutch books are based. Probabilism, conditionalization, and probability kinematics all have Dutch book defenses. In literal terms, you make sure that your credences are probabilities to avoid making stupid bets. Agents who obey the probability norms are said to be coherent, and this is the minimal standard of Bayesian rationality.3
Before going further, I'll give my own amateur opinion - though one many of my superiors share if I judge correctly - on argumentation about Bayesianism. To me, the key defense of Bayesianism is Carnapian; it is a very powerful and readily comprehensible tool. Even if I thought Dutch books complete and miserable failures, I would still be writing these posts. To me, this post is inessential, and I would be entirely uninjured were readers to skip this information. But Dutch books are really interesting, and if you read further, you will run into them. So I should introduce them regardless of whether I deem them inessential, but I am also happy to introduce them for their own sake.2
I think my intuitions about Bayesianism are well-founded. It seems strange to not have a minimal credence, i.e. 0, which applies to necessary falsehoods. I do not think it is sensible to say "I am less committed to an uncertain proposition than I am a necessary falsehood." Similarly, I think it nonsensical to lack a maximum value of commitment: try to imagine committing to an uncertain proposition more strongly than you do a tautology. That credence is one-dimensional and continuous is more difficult; the latter of which is mostly an item of computational convenience, just as continuity in physics is. As Carnap mentions - and I'll trust his knowledge of the physics - our measurements of the world are entirely compatible with strictly rational-valued spacial coordinates, but the loss of continuity would present absurd and unnecessary difficulties in calculation and theory. For one-dimensionality, I think one should always be able to say of two propositions that credence may be compared, i.e. the ordering should be complete as it is on the real numbers. So vector-valued credences should have a real norm. If it is e.g. the max norm, then multi-dimensionality adds no effect. If it is e.g. the standard Euclidean norm on 2-dimensional real vectors, then tautologies would having (1) different credences - the points would lie somewhere on the unit circle in the first quadrant - or (2) the same credence, e.g.
A case of finite additivity - the complement rule - is also intuitive; try saying that you believe in a proposition with 50% confidence and you believe in its negation with a confidence other than 50%. But additivity generally is more difficult to defend with intuitions and pragmatism, and it does the computational work in probability theory. Why should the disjunction of contradictory hypotheses have additive credence?
There is an intuitive, geometric way of looking at this. Picture a normalized Venn diagram, say a unit square or circle. Then the region represented by two disjoint propositions is disconnected within that diagram; (at least) two sub-regions are non-overlapping, e.g. this. Then the sum of the total area is the sum of the disjoint sub-regions. Similarly, when two regions overlap, the `correct' formula for the total area is given by the inclusion/exclusion principle. Additivity also allows us to `slice up' such a diagram (a partition) and not worry about a failure of normalization.
I think that such considerations and the successful application of probability theory in the sciences are sufficient for a cautious acceptance and application of Bayesianism. I am not saying that it is the only appropriate method for credences. I do not think for example that one should always avoid vague probability; I will discuss how Bayesians can deal with vagueness later. But up to assigning particular values, I have found Bayesian credence more than satisfactory. That all said, I can talk about Dutch books.
I'll be lazy and borrow from the SEP supplement:
The Ramsey/de Finetti argument can be illustrated by an example. Suppose that agent A's degrees of belief in S and ~S (written db(S) and db(~S)) are each .51, and, thus that their sum 1.02 (greater than one). On the behavioral interpretation of degrees of belief introduced above, A would be willing to pay db(S) × $1 for a unit wager on S and db(~S) × $1 for a unit wager on ~S. If a bookie B sells both wagers to A for a total of $1.02, the combination would be a synchronic Dutch Book -- synchronic because the wagers could both be entered into at the same time, and a Dutch Book because A would have paid $1.02 on a combination of wagers guaranteed to pay exactly $1. Thus, A would have a guaranteed net loss of $.02
As mentioned before, the colloquial Dutch book argument is `make probabilistic bets or risk a guaranteed loss', but I agree with the SEP article that Dutch book arguments are claims about pragmatic self-defeat in light of the objections and qualifications. In the context of science, we want to avoid distributing our credences in a way that could ensure inaccuracy. (I assume that nature is not a kindly bookie.)
But if violating the probability axioms could ensure defeat, could it not also ensure victory? Yes, as it turns out, and such an eventuality is called a `Czech book' by Hájek: ``Iff you violate probability theory, there exists a specific bad thing (a Dutch Book against you). Iff you violate probability theory, there exists a specific good thing (a Czech Book for you) (p.797). Hájek explores ways of preserving the Dutch Book - I think with success, along with a few other arguments in the article.
I'll leave the interested reader there.4
1. See e.g. (Howson and Urbach, p.75).
2. This section is a quick read, as is the supplement, to give you some idea of what these arguments look like.
3. This standard is very lax. To use a shopworn illustration, a person who believes that the moon is made of cheese with 90% confidence is `rational' in this sense so long as he believes the moon is NOT made of cheese with 10% confidence. Probabilistic accounts of `reasonableness' will be discussed elsewhere.
4. In case the link breaks, the Hájek's article is Arguments for - or against - probabilism? and is readily accessible in several locations via a Google search.
A Primer on Bayesian Philosophy: 1 - Basic axiomatic probability
There are a great many questions philosophically prior to accepting the (mostly) accepted axioms of probability, i.e. Kolmogorov's axioms. But these are incapable of adequate discussion until probability-as-employed is introduced.
This post is going to be formal, even too formal. But this post is not intended to be a one stop shop for the beginner to comprehend probability. Instead, the beginner should scan this post and use it as a Bayesianism-focused reference while studying the first few chapters of a traditional undergraduate probability textbook or some other professional work.4 Do not feel the need to understand everything here before proceeding further.
As I explain in the next post, the central idea of Bayesianism is the representation of credence, the strength of commitment to a proposition, by a non-zero real number [see (1)]. When encountering this idea and axioms of probability, think about what Bayesianism assumes in doing so. Ask yourself, for example, why negative reals do not represent credence. Think of what one could gain - if anything -by doing so. Ask yourself whether credence should lie on the real interval at all. Why not the rational numbers? Why not a vector space (to allow multi-dimensional values)? Why employ the continuum? Why should credence be normalizable [see (2)]?
I hope to discuss most of these questions in detail later, but I hope those encountering the axioms now will prefer honest toil to theft and think about why these postulates are postulated.
First, some notes on notation. The subset symbol `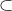
' denotes general inclusion, not strict inclusion. I denote 
for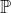 
the set of positive integers. This is much more elegant than the explicit version, and the symbol for the positive numbers helps diminish confusion with the natural numbers (non-negative integers).
As I am more comfortable with set notation, I introduce the topic as such, but it is possible to rewrite what follows in propositional form. It is quite common to encounter this, but the difference is symbolic.5 Conjunction, disjunction, `and', `or', negation, etc. may be substituted as needed.
Let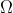
denote the sample space, the set of possibilities, subsets of which are called events. For a simple coin toss, the sample space is 
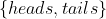, and the set of events is the powerset 
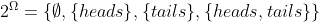. An event occurs if an element occurs. Then p is a probability function on if it satisfies the following: \subset 2^\Omega "Domain(p)\subset 2^\Omega")
is closed under set complement, and
1. Positivity:\implies 0\leq p(E)\in\mathbb{R} "E\in Domain(p)\implies 0\leq p(E)\in\mathbb{R}")
.
2. Normalizability:
3. Finite additivity:\implies p(E\cup F)=p(E)+p(F) "E,F,,E\cup F\in Domain(p)\implies p(E\cup F)=p(E)+p(F)")
Those familiar with probability theory will notice certain differences from a standard presentation. Note that p is defined on subsets of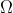, but I have not assumed that it is defined on 
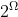or a sigma-field of its subsets. The only general assumption about Domain(p) which I make is that it is closed up to complements, i.e. \implies E^c\in Domain(p) "E\in Domain(p)\implies E^c\in Domain(p)")
. Axiom (3) is a weakening of countable additivity. Usually, (3) is introduced as countable additivity:
3*. Countable additivity: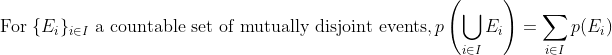
.
(Note that I have ceased to make the domain assumptions explicit.) It is an elementary theorem that (1), (2), and (3*) entail (3). But accepting countable additivity, along with assuming that Domain(p) is a sigma-field, may assume too much. For purposes of simplification, I will implicitly assume that p is defined on all subsets of the sample space. But as we will see in later sections, this is not necessarily the case.1 And of course, one may generalize probability further, but that would require more advanced mathematics, i.e. measure theory.
To understand the appeal of these axioms, it is important to remember that they are relatively young: Kolmogorov first published them in 1933. Before, probabilities were defined as relative frequencies, i.e.
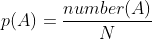
where number(A) denotes the number of occurrences of A in N trials, or limiting long run frequencies, i.e.
.
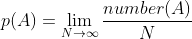One notices several problems with these notions. For the latter, the assumption that a limit exists is required. For both, N counts a reference class of events which requires specification, and reference classes are not always clear.2 There are also counter-factual commitments implicit in the definition, e.g. `if you were to toss this coin ad infinitum...' Worse still, relative frequency presupposes the uniform distribution and a finite sample space, and not all possibilities are equiprobable. But the Kolmogorov axioms capture such notions, where applicable.
Before going further, conditional probabilities need to be introduced. Very often, conditional probability is presented as a definition, and not an analysis - which it almost always is in practice. Usually, it is given in ratio analysis form:
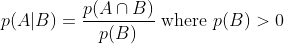
The assumption that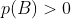
may be dispensed with when given in multiplication law form:
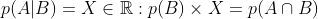
As the ratio `definition' is most common, I accept it as the default, with caution as to its shortcomings.3 When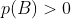, the ratio definition allows a quick proof that p(.|B) is itself a probability, a process known as reduction of sample space. The multiplication law also easily follows from the ratio form.
Theorem List
In what follows, probabilities are assumed to be defined wherever they appear. Items marked with an asterisk require countable additivity. [I currently see no need to include such theorems, some of which (e.g. continuity with respect to series of subsets and supersets) require calculus.] Unless stated otherwise, theorems follow from (1)-(3) and the ratio analysis of conditional probability. I will state these theorems in logical order; their derivation can be found in any elementary probability textbook, although many needlessly invoke countable additivity in the process.
Equivalence condition.=p(B) "A=B\implies p(A)=p(B)")
Probability of impossibility.=0 "p(\emptyset)=0")
. Note that the converse does not hold: some probabilities assign probability 0 to non-empty events, just as some probabilities assign probability 1 to uncertain events. Such events are said to almost never occur and almost surely occur, respectively. There are some philosophical difficulties with such events, as I discuss later. Many Bayesians employ the regularity norm (an unfortunate name), which states that uncertain events always have positive probability.
Complement rule.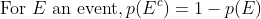
This follows by noticing that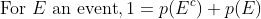
, a rule which can be generalized to account for larger partitions of .
Subset rule.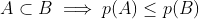
Finite additivity.=\sum_{i\in[n]}p(E_i) "\text{For }\{E_i\}_{i\in[n]}\text{ a set of mutually disjoint events, }p\left(\cup_{i\in[n]}E_i \right)=\sum_{i\in[n]}p(E_i)")
Inclusion/Exclusion Principle.
This is often encountered in its simpler form: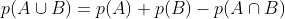
Law of Total Probability.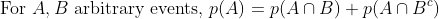
This has a ready generalization:
Which has an equivalent in terms of conditional probability:
Multiplication law. For
a set of events in which arbitrary intersections have nonzero probability,
=p(E_1)p(E_2|E_1)\times\cdots\times p(E_n|E_1\cap\cdots\cap E_{n-1}) "p(\cap_{i\in[n]}E_i)=p(E_1)p(E_2|E_1)\times\cdots\times p(E_n|E_1\cap\cdots\cap E_{n-1})")
Sample space reduction. p(B)>0 implies that "p(\cdot|B)")
is itself a probability map [over Domain(p)]. I.e., satisfies (1)-(3) and therefore satisfies each of the previous theorems.
Bayes' Theorem.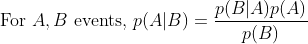
This may be generalized using the Law of Total Probability:
=\frac{p(B|A_i)p(A_i)}{\sum_{j\in[n]}p(A_j)p(B|A_j)} "p(A_i|B)=\frac{p(B|A_i)p(A_i)}{\sum_{j\in[n]}p(A_j)p(B|A_j)}")
Of great importance is the odds form of Bayes' Theorem: for H a hypothesis and E some evidence,
}{p(H^c|E)}=\frac{p(E|H)}{p(E|H^c)}\frac{p(H)}{p(H^c)} "\frac{p(H|E)}{p(H^c|E)}=\frac{p(E|H)}{p(E|H^c)}\frac{p(H)}{p(H^c)}")
In this form, the term}{p(H^c|E)} "\frac{p(H|E)}{p(H^c|E)}")
is called the posterior odds on H, }{p(E|H^c)} "\frac{p(E|H)}{p(E|H^c)}")
the Bayes' factor, and }{p(H^c)} "\frac{p(H)}{p(H^c)}")
the prior odds on H. The significance of the terminology is explained in the next post.
1. The subjective interpretation of probability allows for this. It is possible to be separately committed to events
.
2. This is discussed further in the subjective/objective post.
3. See e.g. Alan Hájek's What Conditional Probability Could not Be.
4. I largely follow Colin Howson and Peter Urbach. Scientific Reasoning: The Bayesian Approach. Open Court: La Salle, 1989.
5. ibid, pp.18-9.
This post is going to be formal, even too formal. But this post is not intended to be a one stop shop for the beginner to comprehend probability. Instead, the beginner should scan this post and use it as a Bayesianism-focused reference while studying the first few chapters of a traditional undergraduate probability textbook or some other professional work.4 Do not feel the need to understand everything here before proceeding further.
As I explain in the next post, the central idea of Bayesianism is the representation of credence, the strength of commitment to a proposition, by a non-zero real number [see (1)]. When encountering this idea and axioms of probability, think about what Bayesianism assumes in doing so. Ask yourself, for example, why negative reals do not represent credence. Think of what one could gain - if anything -by doing so. Ask yourself whether credence should lie on the real interval at all. Why not the rational numbers? Why not a vector space (to allow multi-dimensional values)? Why employ the continuum? Why should credence be normalizable [see (2)]?
I hope to discuss most of these questions in detail later, but I hope those encountering the axioms now will prefer honest toil to theft and think about why these postulates are postulated.
First, some notes on notation. The subset symbol `
As I am more comfortable with set notation, I introduce the topic as such, but it is possible to rewrite what follows in propositional form. It is quite common to encounter this, but the difference is symbolic.5 Conjunction, disjunction, `and', `or', negation, etc. may be substituted as needed.
Let
1. Positivity:
2. Normalizability:
3. Finite additivity:
Those familiar with probability theory will notice certain differences from a standard presentation. Note that p is defined on subsets of
3*. Countable additivity:
(Note that I have ceased to make the domain assumptions explicit.) It is an elementary theorem that (1), (2), and (3*) entail (3). But accepting countable additivity, along with assuming that Domain(p) is a sigma-field, may assume too much. For purposes of simplification, I will implicitly assume that p is defined on all subsets of the sample space. But as we will see in later sections, this is not necessarily the case.1 And of course, one may generalize probability further, but that would require more advanced mathematics, i.e. measure theory.
To understand the appeal of these axioms, it is important to remember that they are relatively young: Kolmogorov first published them in 1933. Before, probabilities were defined as relative frequencies, i.e.
where number(A) denotes the number of occurrences of A in N trials, or limiting long run frequencies, i.e.
One notices several problems with these notions. For the latter, the assumption that a limit exists is required. For both, N counts a reference class of events which requires specification, and reference classes are not always clear.2 There are also counter-factual commitments implicit in the definition, e.g. `if you were to toss this coin ad infinitum...' Worse still, relative frequency presupposes the uniform distribution and a finite sample space, and not all possibilities are equiprobable. But the Kolmogorov axioms capture such notions, where applicable.
Before going further, conditional probabilities need to be introduced. Very often, conditional probability is presented as a definition, and not an analysis - which it almost always is in practice. Usually, it is given in ratio analysis form:
The assumption that
As the ratio `definition' is most common, I accept it as the default, with caution as to its shortcomings.3 When
Theorem List
In what follows, probabilities are assumed to be defined wherever they appear. Items marked with an asterisk require countable additivity. [I currently see no need to include such theorems, some of which (e.g. continuity with respect to series of subsets and supersets) require calculus.] Unless stated otherwise, theorems follow from (1)-(3) and the ratio analysis of conditional probability. I will state these theorems in logical order; their derivation can be found in any elementary probability textbook, although many needlessly invoke countable additivity in the process.
Equivalence condition.
Probability of impossibility.
Complement rule.
This follows by noticing that
Subset rule.
Finite additivity.
Inclusion/Exclusion Principle.
This is often encountered in its simpler form:
Law of Total Probability.
This has a ready generalization:
Which has an equivalent in terms of conditional probability:
Multiplication law. For
Sample space reduction. p(B)>0 implies that
Bayes' Theorem.
This may be generalized using the Law of Total Probability:
Of great importance is the odds form of Bayes' Theorem: for H a hypothesis and E some evidence,
In this form, the term
1. The subjective interpretation of probability allows for this. It is possible to be separately committed to events
2. This is discussed further in the subjective/objective post.
3. See e.g. Alan Hájek's What Conditional Probability Could not Be.
4. I largely follow Colin Howson and Peter Urbach. Scientific Reasoning: The Bayesian Approach. Open Court: La Salle, 1989.
5. ibid, pp.18-9.
Subscribe to:
Posts (Atom)